Generating peak-aware pseudo-measurements for low-voltage feeders using metadata of distribution system operators

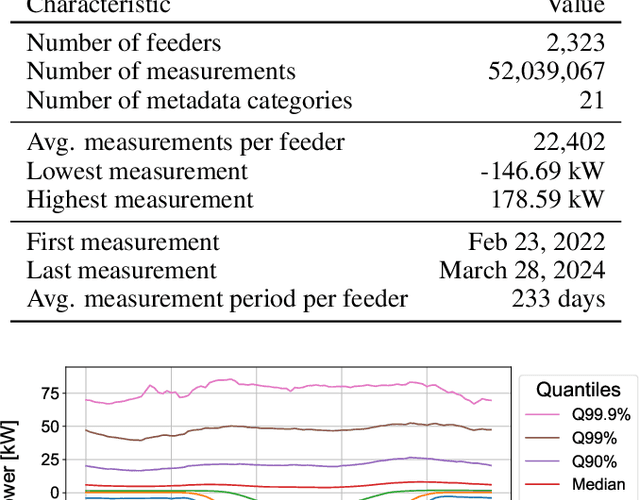
Distribution system operators (DSOs) must cope with new challenges such as the reconstruction of distribution grids along climate neutrality pathways or the ability to manage and control consumption and generation in the grid. In order to meet the challenges, measurements within the distribution grid often form the basis for DSOs. Hence, it is an urgent problem that measurement devices are not installed in many low-voltage (LV) grids. In order to overcome this problem, we present an approach to estimate pseudo-measurements for non-measured LV feeders based on the metadata of the respective feeder using regression models. The feeder metadata comprise information about the number of grid connection points, the installed power of consumers and producers, and billing data in the downstream LV grid. Additionally, we use weather data, calendar data and timestamp information as model features. The existing measurements are used as model target. We extensively evaluate the estimated pseudo-measurements on a large real-world dataset with 2,323 LV feeders characterized by both consumption and feed-in. For this purpose, we introduce peak metrics inspired by the BigDEAL challenge for the peak magnitude, timing and shape for both consumption and feed-in. As regression models, we use XGBoost, a multilayer perceptron (MLP) and a linear regression (LR). We observe that XGBoost and MLP outperform the LR. Furthermore, the results show that the approach adapts to different weather, calendar and timestamp conditions and produces realistic load curves based on the feeder metadata. In the future, the approach can be adapted to other grid levels like substation transformers and can supplement research fields like load modeling, state estimation and LV load forecasting.

The Mean Dimension of Neural Networks -- What causes the interaction effects?

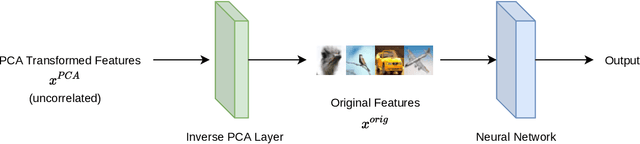
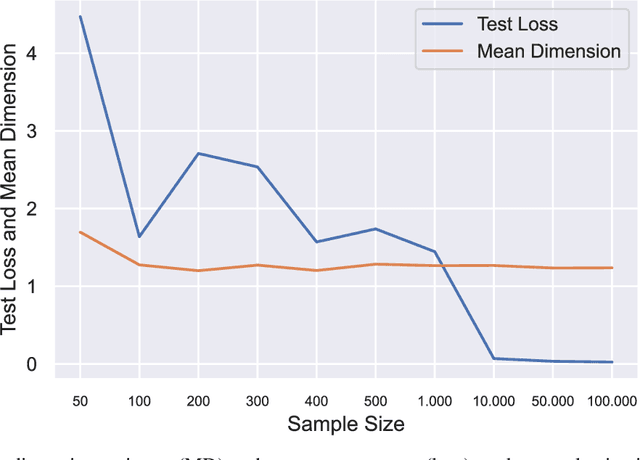
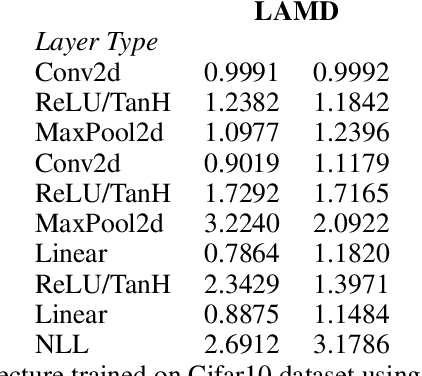
Owen and Hoyt recently showed that the effective dimension offers key structural information about the input-output mapping underlying an artificial neural network. Along this line of research, this work proposes an estimation procedure that allows the calculation of the mean dimension from a given dataset, without resampling from external distributions. The design yields total indices when features are independent and a variant of total indices when features are correlated. We show that this variant possesses the zero independence property. With synthetic datasets, we analyse how the mean dimension evolves layer by layer and how the activation function impacts the magnitude of interactions. We then use the mean dimension to study some of the most widely employed convolutional architectures for image recognition (LeNet, ResNet, DenseNet). To account for pixel correlations, we propose calculating the mean dimension after the addition of an inverse PCA layer that allows one to work on uncorrelated PCA-transformed features, without the need to retrain the neural network. We use the generalized total indices to produce heatmaps for post-hoc explanations, and we employ the mean dimension on the PCA-transformed features for cross comparisons of the artificial neural networks structures. Results provide several insights on the difference in magnitude of interactions across the architectures, as well as indications on how the mean dimension evolves during training.