The Mean Dimension of Neural Networks -- What causes the interaction effects?
Paper and Code
Jul 11, 2022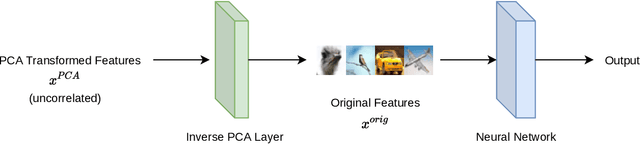

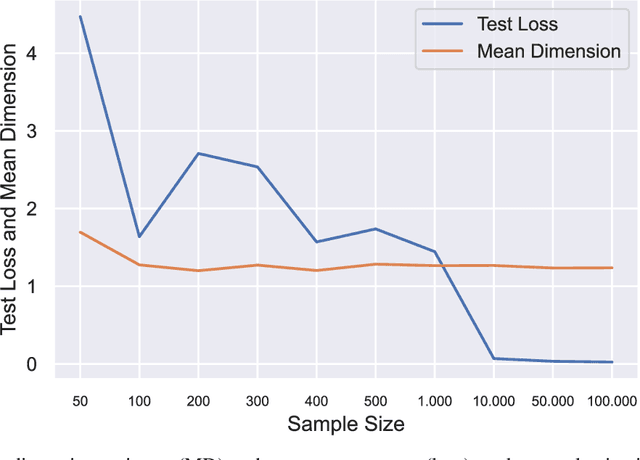
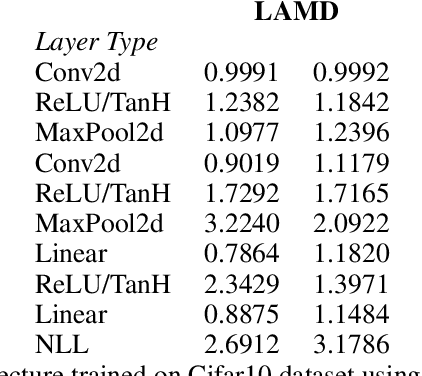
Owen and Hoyt recently showed that the effective dimension offers key structural information about the input-output mapping underlying an artificial neural network. Along this line of research, this work proposes an estimation procedure that allows the calculation of the mean dimension from a given dataset, without resampling from external distributions. The design yields total indices when features are independent and a variant of total indices when features are correlated. We show that this variant possesses the zero independence property. With synthetic datasets, we analyse how the mean dimension evolves layer by layer and how the activation function impacts the magnitude of interactions. We then use the mean dimension to study some of the most widely employed convolutional architectures for image recognition (LeNet, ResNet, DenseNet). To account for pixel correlations, we propose calculating the mean dimension after the addition of an inverse PCA layer that allows one to work on uncorrelated PCA-transformed features, without the need to retrain the neural network. We use the generalized total indices to produce heatmaps for post-hoc explanations, and we employ the mean dimension on the PCA-transformed features for cross comparisons of the artificial neural networks structures. Results provide several insights on the difference in magnitude of interactions across the architectures, as well as indications on how the mean dimension evolves during training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge