Autonomous Quadrotor Landing using Deep Reinforcement Learning

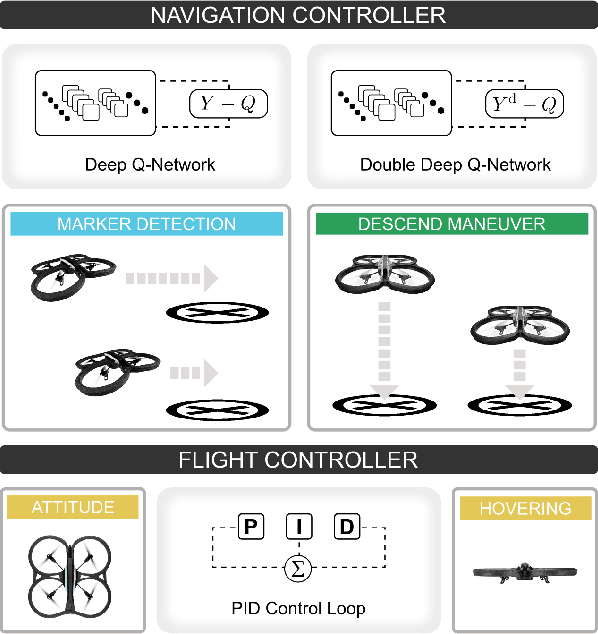
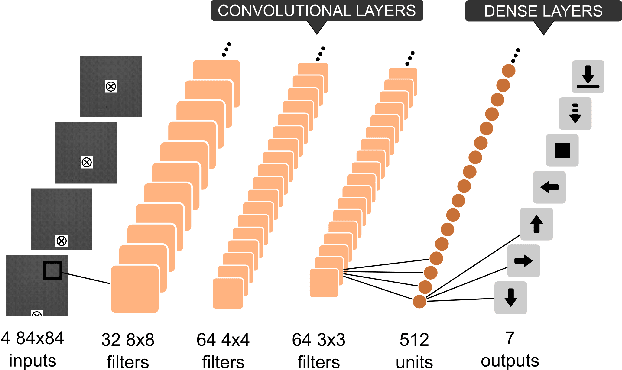
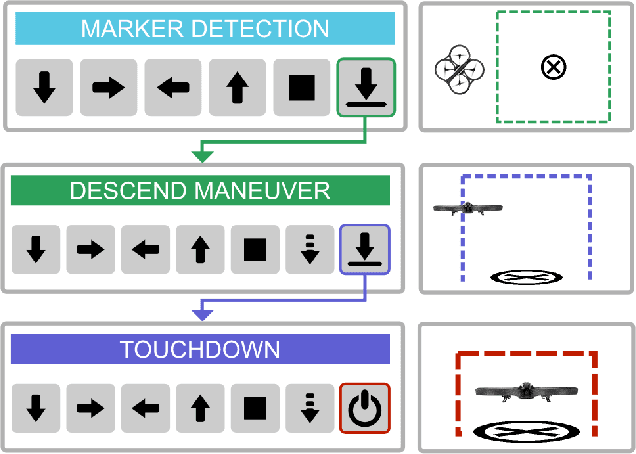
Landing an unmanned aerial vehicle (UAV) on a ground marker is an open problem despite the effort of the research community. Previous attempts mostly focused on the analysis of hand-crafted geometric features and the use of external sensors in order to allow the vehicle to approach the land-pad. In this article, we propose a method based on deep reinforcement learning that only requires low-resolution images taken from a down-looking camera in order to identify the position of the marker and land the UAV on it. The proposed approach is based on a hierarchy of Deep Q-Networks (DQNs) used as high-level control policy for the navigation toward the marker. We implemented different technical solutions, such as the combination of vanilla and double DQNs, and a partitioned buffer replay. Using domain randomization we trained the vehicle on uniform textures and we tested it on a large variety of simulated and real-world environments. The overall performance is comparable with a state-of-the-art algorithm and human pilots.

Monocular Visual Odometry for an Unmanned Sea-Surface Vehicle

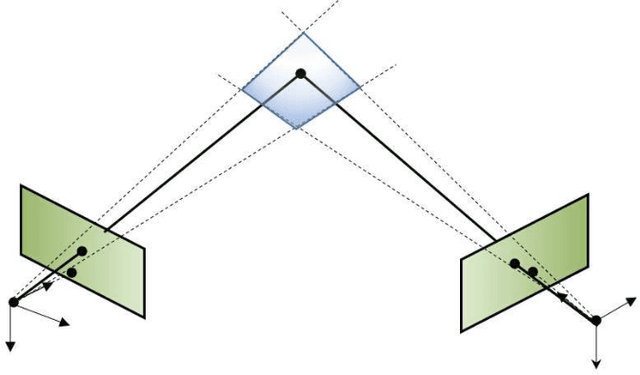
We tackle the problem of localizing an autonomous sea-surface vehicle in river estuarine areas using monocular camera and angular velocity input from an inertial sensor. Our method is challenged by two prominent drawbacks associated with the environment, which are typically not present in standard visual simultaneous localization and mapping (SLAM) applications on land (or air): a) Scene depth varies significantly (from a few meters to several kilometers) and, b) In conjunction to the latter, there exists no ground plane to provide features with enough disparity based on which to reliably detect motion. To that end, we use the IMU orientation feedback in order to re-cast the problem of visual localization without the mapping component, although the map can be implicitly obtained from the camera pose estimates. We find that our method produces reliable odometry estimates for trajectories several hundred meters long in the water. To compare the visual odometry estimates with GPS based ground truth, we interpolate the trajectory with splines on a common parameter and obtain position error in meters recovering an optimal affine transformation between the two splines.