Harnessing and modulating chaos to sample from neural generative models

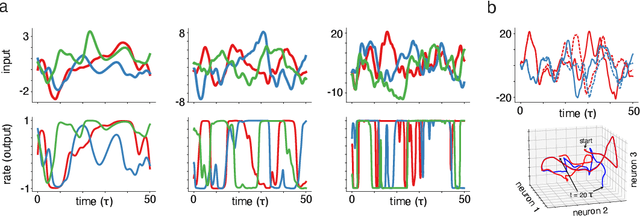
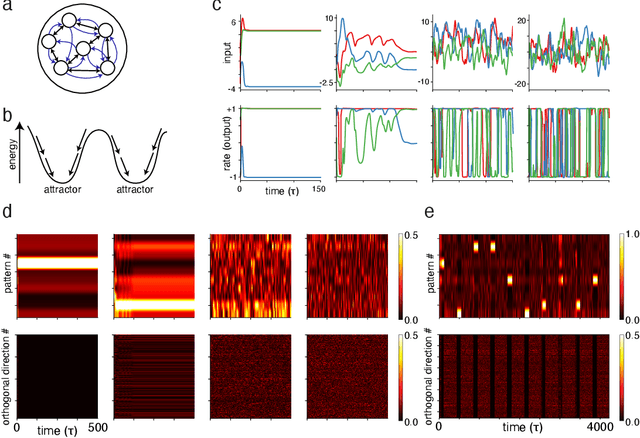
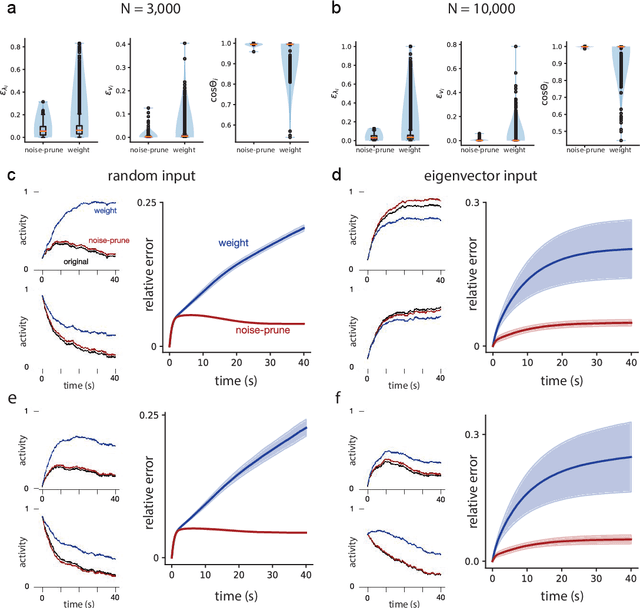
Chaos is generic in strongly-coupled recurrent networks of model neurons, and thought to be an easily accessible dynamical regime in the brain. While neural chaos is typically seen as an impediment to robust computation, we show how such chaos might play a functional role in allowing the brain to learn and sample from generative models. We construct architectures that combine a classic model of neural chaos either with a canonical generative modeling architecture or with energy-based models of neural memory. We show that these architectures have appealing properties for sampling, including easy biologically-plausible control of sampling rates via overall gain modulation.

Towards Reverse-Engineering the Brain: Brain-Derived Neuromorphic Computing Approach with Photonic, Electronic, and Ionic Dynamicity in 3D integrated circuits

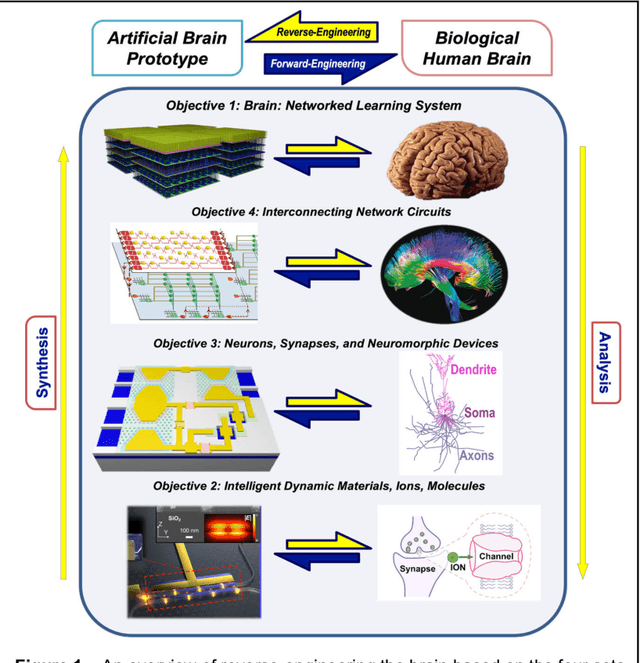
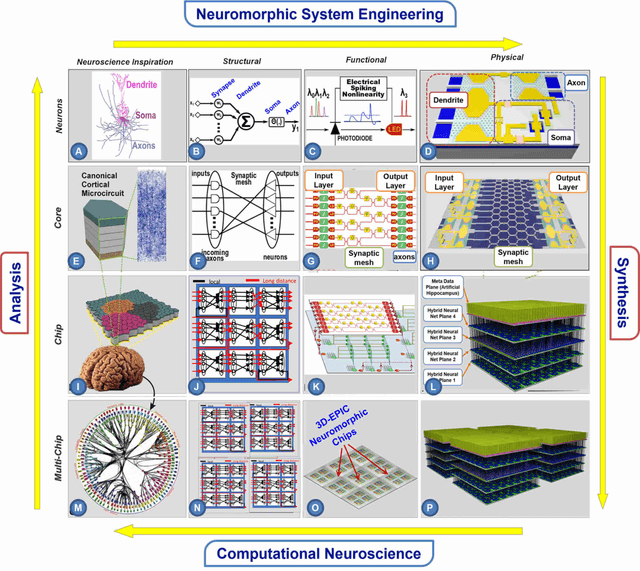
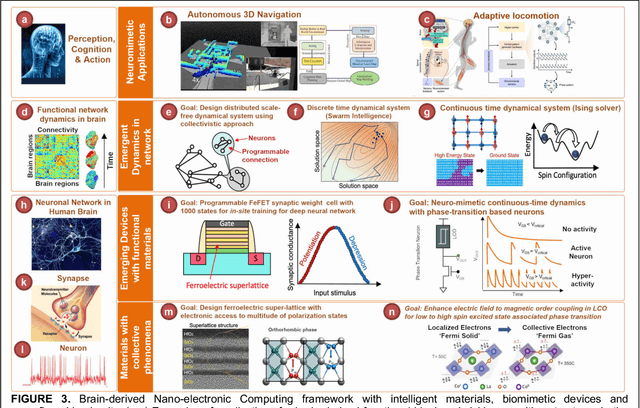
The human brain has immense learning capabilities at extreme energy efficiencies and scale that no artificial system has been able to match. For decades, reverse engineering the brain has been one of the top priorities of science and technology research. Despite numerous efforts, conventional electronics-based methods have failed to match the scalability, energy efficiency, and self-supervised learning capabilities of the human brain. On the other hand, very recent progress in the development of new generations of photonic and electronic memristive materials, device technologies, and 3D electronic-photonic integrated circuits (3D EPIC ) promise to realize new brain-derived neuromorphic systems with comparable connectivity, density, energy-efficiency, and scalability. When combined with bio-realistic learning algorithms and architectures, it may be possible to realize an 'artificial brain' prototype with general self-learning capabilities. This paper argues the possibility of reverse-engineering the brain through architecting a prototype of a brain-derived neuromorphic computing system consisting of artificial electronic, ionic, photonic materials, devices, and circuits with dynamicity resembling the bio-plausible molecular, neuro/synaptic, neuro-circuit, and multi-structural hierarchical macro-circuits of the brain based on well-tested computational models. We further argue the importance of bio-plausible local learning algorithms applicable to the neuromorphic computing system that capture the flexible and adaptive unsupervised and self-supervised learning mechanisms central to human intelligence. Most importantly, we emphasize that the unique capabilities in brain-derived neuromorphic computing prototype systems will enable us to understand links between specific neuronal and network-level properties with system-level functioning and behavior.

Adaptive Synaptic Failure Enables Sampling from Posterior Predictive Distributions in the Brain

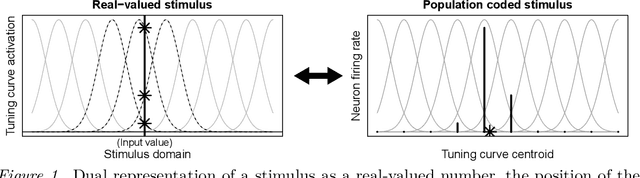
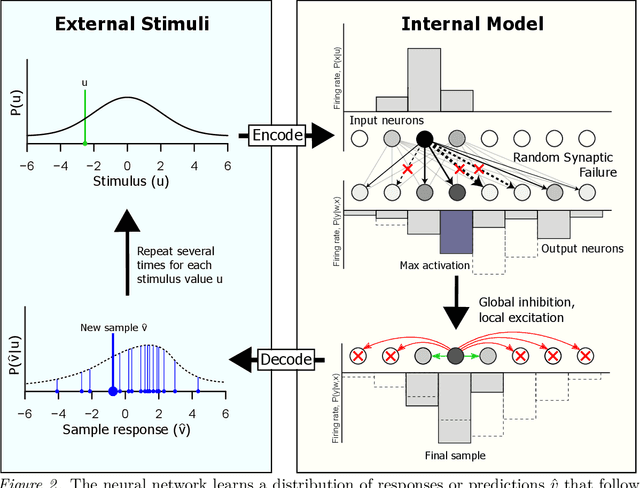
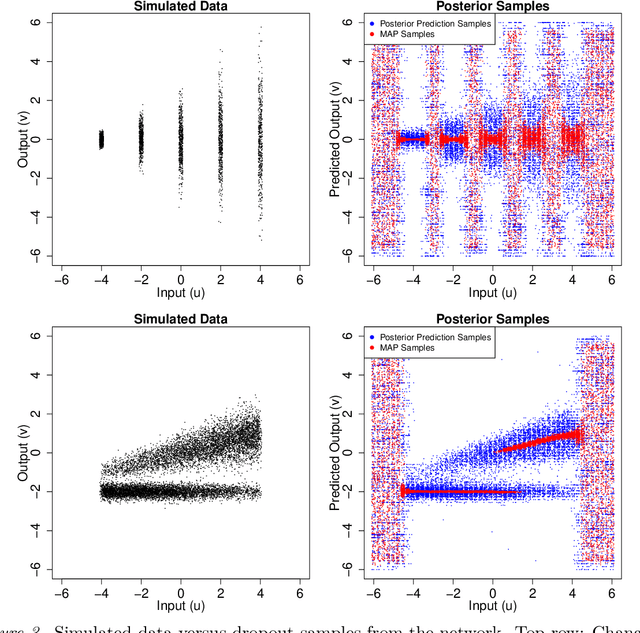
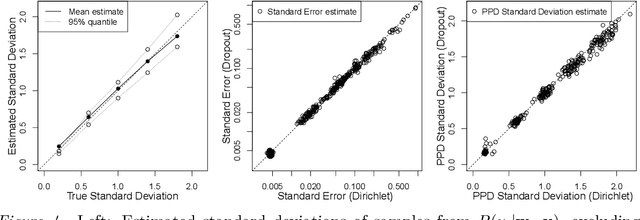
Bayesian interpretations of neural processing require that biological mechanisms represent and operate upon probability distributions in accordance with Bayes' theorem. Many have speculated that synaptic failure constitutes a mechanism of variational, i.e., approximate, Bayesian inference in the brain. Whereas models have previously used synaptic failure to sample over uncertainty in model parameters, we demonstrate that by adapting transmission probabilities to learned network weights, synaptic failure can sample not only over model uncertainty, but complete posterior predictive distributions as well. Our results potentially explain the brain's ability to perform probabilistic searches and to approximate complex integrals. These operations are involved in numerous calculations, including likelihood evaluation and state value estimation for complex planning.

Locally Learned Synaptic Dropout for Complete Bayesian Inference

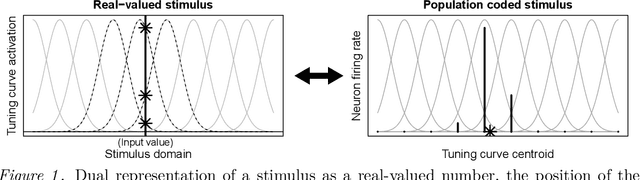
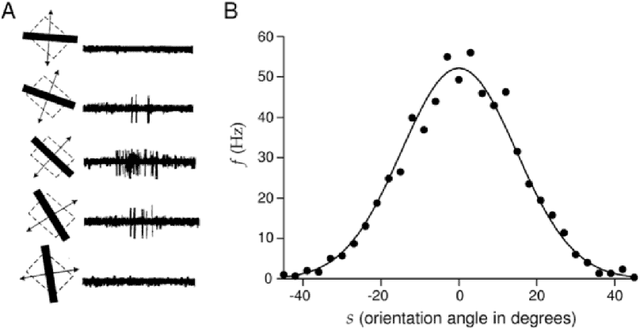
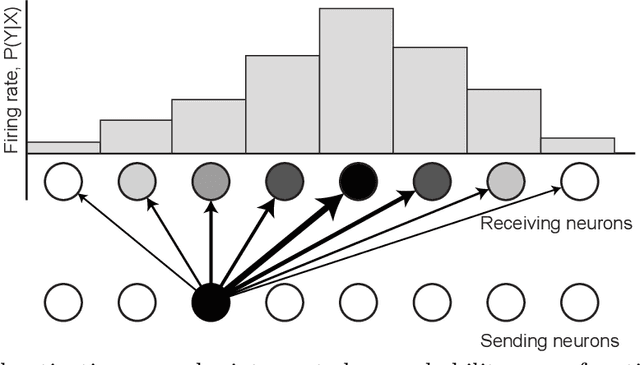
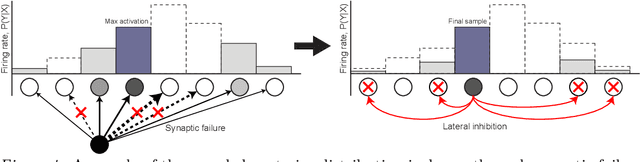
The Bayesian brain hypothesis postulates that the brain accurately operates on statistical distributions according to Bayes' theorem. The random failure of presynaptic vesicles to release neurotransmitters may allow the brain to sample from posterior distributions of network parameters, interpreted as epistemic uncertainty. It has not been shown previously how random failures might allow networks to sample from observed distributions, also known as aleatoric or residual uncertainty. Sampling from both distributions enables probabilistic inference, efficient search, and creative or generative problem solving. We demonstrate that under a population-code based interpretation of neural activity, both types of distribution can be represented and sampled with synaptic failure alone. We first define a biologically constrained neural network and sampling scheme based on synaptic failure and lateral inhibition. Within this framework, we derive drop-out based epistemic uncertainty, then prove an analytic mapping from synaptic efficacy to release probability that allows networks to sample from arbitrary, learned distributions represented by a receiving layer. Second, our result leads to a local learning rule by which synapses adapt their release probabilities. Our result demonstrates complete Bayesian inference, related to the variational learning method of dropout, in a biologically constrained network using only locally-learned synaptic failure rates.

Using noise to probe recurrent neural network structure and prune synapses

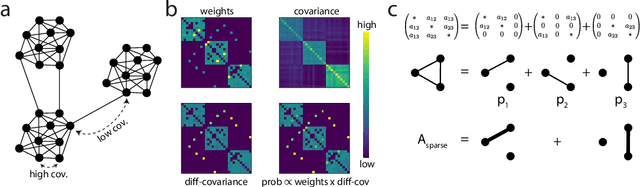
Many networks in the brain are sparsely connected, and the brain eliminates synapses during development and learning. How could the brain decide which synapses to prune? In a recurrent network, determining the importance of a synapse between two neurons is a difficult computational problem, depending on the role that both neurons play and on all possible pathways of information flow between them. Noise is ubiquitous in neural systems, and often considered an irritant to be overcome. Here we suggest that noise could play a functional role in synaptic pruning, allowing the brain to probe network structure and determine which synapses are redundant. We construct a simple, local, unsupervised plasticity rule that either strengthens or prunes synapses using only synaptic weight and the noise-driven covariance of the neighboring neurons. For a subset of linear and rectified-linear networks, we prove that this rule preserves the spectrum of the original matrix and hence preserves network dynamics even when the fraction of pruned synapses asymptotically approaches 1. The plasticity rule is biologically-plausible and may suggest a new role for noise in neural computation.

Associative content-addressable networks with exponentially many robust stable states

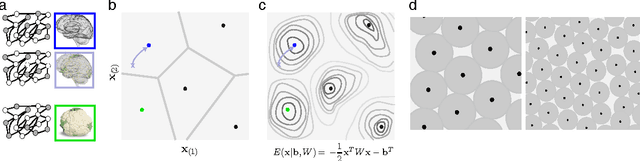
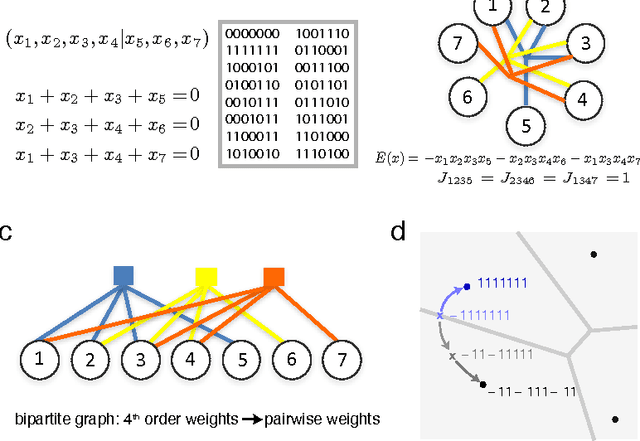
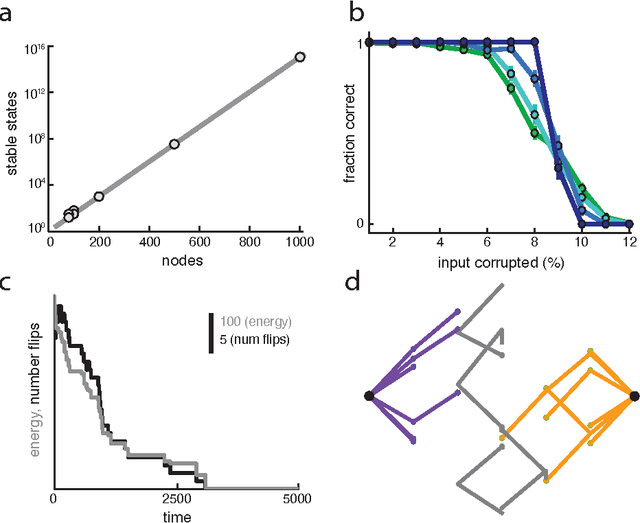
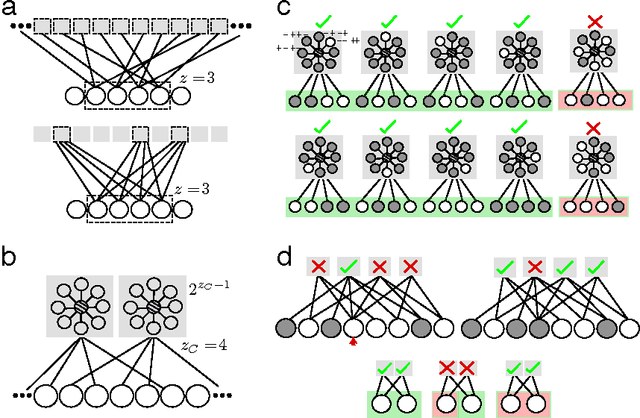
The brain must robustly store a large number of memories, corresponding to the many events encountered over a lifetime. However, the number of memory states in existing neural network models either grows weakly with network size or recall fails catastrophically with vanishingly little noise. We construct an associative content-addressable memory with exponentially many stable states and robust error-correction. The network possesses expander graph connectivity on a restricted Boltzmann machine architecture. The expansion property allows simple neural network dynamics to perform at par with modern error-correcting codes. Appropriate networks can be constructed with sparse random connections, glomerular nodes, and associative learning using low dynamic-range weights. Thus, sparse quasi-random structures---characteristic of important error-correcting codes---may provide for high-performance computation in artificial neural networks and the brain.