Thinking agents for zero-shot generalization to qualitatively novel tasks

Intelligent organisms can solve truly novel problems which they have never encountered before, either in their lifetime or their evolution. An important component of this capacity is the ability to ``think'', that is, to mentally manipulate objects, concepts and behaviors in order to plan and evaluate possible solutions to novel problems, even without environment interaction. To generate problems that are truly qualitatively novel, while still solvable zero-shot (by mental simulation), we use the combinatorial nature of environments: we train the agent while withholding a specific combination of the environment's elements. The novel test task, based on this combination, is thus guaranteed to be truly novel, while still mentally simulable since the agent has been exposed to each individual element (and their pairwise interactions) during training. We propose a method to train agents endowed with world models to make use their mental simulation abilities, by selecting tasks based on the difference between the agent's pre-thinking and post-thinking performance. When tested on the novel, withheld problem, the resulting agent successfully simulated alternative scenarios and used the resulting information to guide its behavior in the actual environment, solving the novel task in a single real-environment trial (zero-shot).

A Method of Selective Attention for Reservoir Based Agents

Training of deep reinforcement learning agents is slowed considerably by the presence of input dimensions that do not usefully condition the reward function. Existing modules such as layer normalization can be trained with weight decay to act as a form of selective attention, i.e. an input mask, that shrinks the scale of unnecessary inputs, which in turn accelerates training of the policy. However, we find a surprising result that adding numerous parameters to the computation of the input mask results in much faster training. A simple, high dimensional masking module is compared with layer normalization and a model without any input suppression. The high dimensional mask resulted in a four-fold speedup in training over the null hypothesis and a two-fold speedup in training over the layer normalization method.

LearnLM: Improving Gemini for Learning

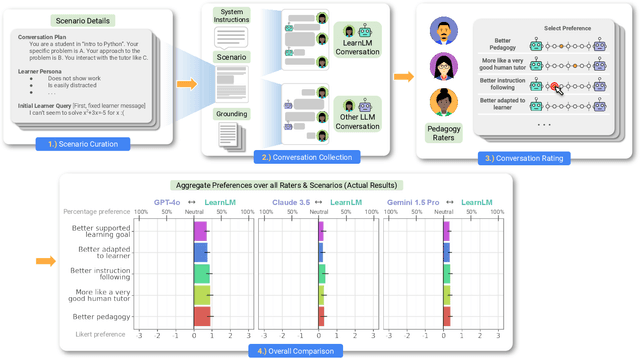
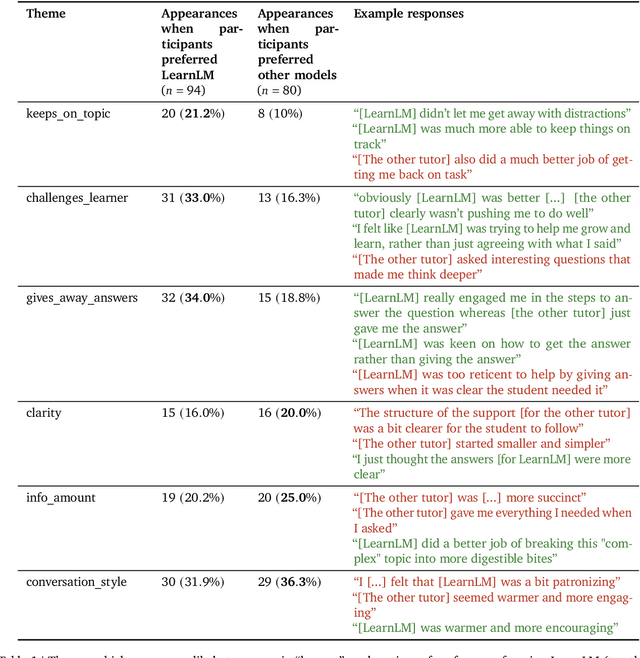
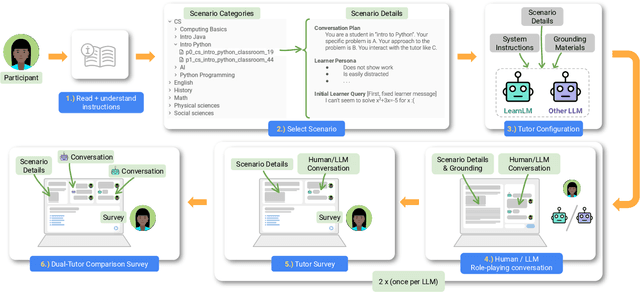
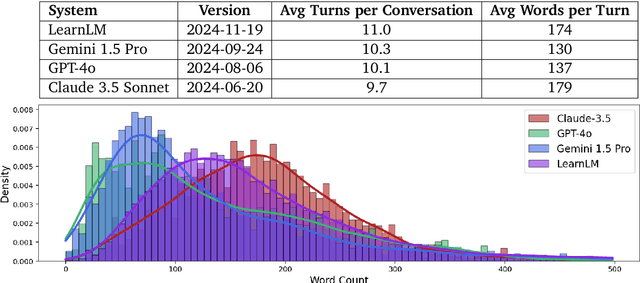
Today's generative AI systems are tuned to present information by default rather than engage users in service of learning as a human tutor would. To address the wide range of potential education use cases for these systems, we reframe the challenge of injecting pedagogical behavior as one of \textit{pedagogical instruction following}, where training and evaluation examples include system-level instructions describing the specific pedagogy attributes present or desired in subsequent model turns. This framing avoids committing our models to any particular definition of pedagogy, and instead allows teachers or developers to specify desired model behavior. It also clears a path to improving Gemini models for learning -- by enabling the addition of our pedagogical data to post-training mixtures -- alongside their rapidly expanding set of capabilities. Both represent important changes from our initial tech report. We show how training with pedagogical instruction following produces a LearnLM model (available on Google AI Studio) that is preferred substantially by expert raters across a diverse set of learning scenarios, with average preference strengths of 31\% over GPT-4o, 11\% over Claude 3.5, and 13\% over the Gemini 1.5 Pro model LearnLM was based on.

Reservoir Computing for Fast, Simplified Reinforcement Learning on Memory Tasks

Tasks in which rewards depend upon past information not available in the current observation set can only be solved by agents that are equipped with short-term memory. Usual choices for memory modules include trainable recurrent hidden layers, often with gated memory. Reservoir computing presents an alternative, in which a recurrent layer is not trained, but rather has a set of fixed, sparse recurrent weights. The weights are scaled to produce stable dynamical behavior such that the reservoir state contains a high-dimensional, nonlinear impulse response function of the inputs. An output decoder network can then be used to map the compressive history represented by the reservoir's state to any outputs, including agent actions or predictions. In this study, we find that reservoir computing greatly simplifies and speeds up reinforcement learning on memory tasks by (1) eliminating the need for backpropagation of gradients through time, (2) presenting all recent history simultaneously to the downstream network, and (3) performing many useful and generic nonlinear computations upstream from the trained modules. In particular, these findings offer significant benefit to meta-learning that depends primarily on efficient and highly general memory systems.

Adaptive Synaptic Failure Enables Sampling from Posterior Predictive Distributions in the Brain

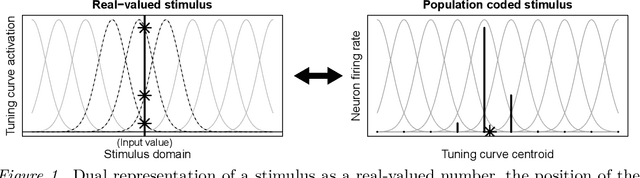
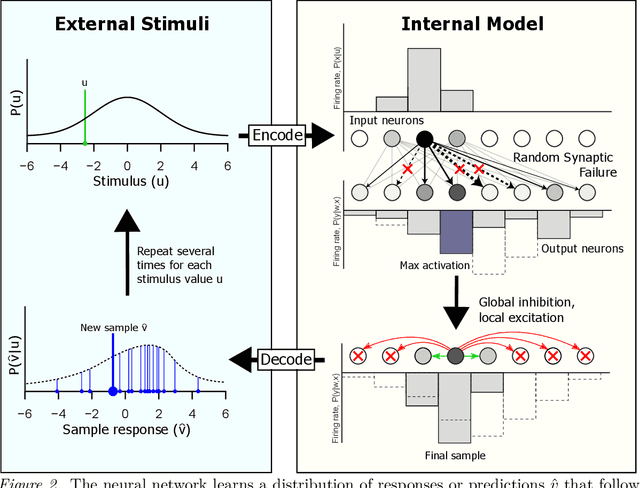
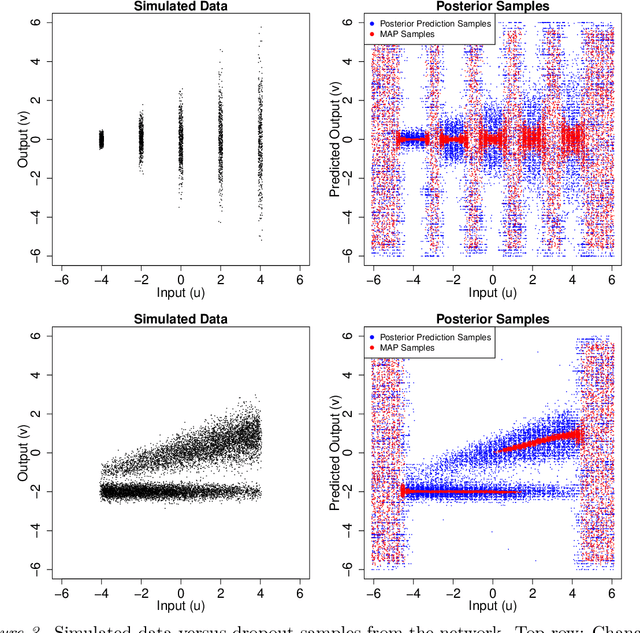
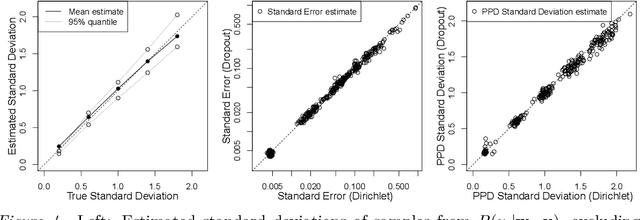
Bayesian interpretations of neural processing require that biological mechanisms represent and operate upon probability distributions in accordance with Bayes' theorem. Many have speculated that synaptic failure constitutes a mechanism of variational, i.e., approximate, Bayesian inference in the brain. Whereas models have previously used synaptic failure to sample over uncertainty in model parameters, we demonstrate that by adapting transmission probabilities to learned network weights, synaptic failure can sample not only over model uncertainty, but complete posterior predictive distributions as well. Our results potentially explain the brain's ability to perform probabilistic searches and to approximate complex integrals. These operations are involved in numerous calculations, including likelihood evaluation and state value estimation for complex planning.