O3SLM: Open Weight, Open Data, and Open Vocabulary Sketch-Language Model

While Large Vision Language Models (LVLMs) are increasingly deployed in real-world applications, their ability to interpret abstract visual inputs remains limited. Specifically, they struggle to comprehend hand-drawn sketches, a modality that offers an intuitive means of expressing concepts that are difficult to describe textually. We identify the primary bottleneck as the absence of a large-scale dataset that jointly models sketches, photorealistic images, and corresponding natural language instructions. To address this, we present two key contributions: (1) a new, large-scale dataset of image-sketch-instruction triplets designed to facilitate both pretraining and instruction tuning, and (2) O3SLM, an LVLM trained on this dataset. Comprehensive evaluations on multiple sketch-based tasks: (a) object localization, (b) counting, (c) image retrieval i.e., (SBIR and fine-grained SBIR), and (d) visual question answering (VQA); while incorporating the three existing sketch datasets, namely QuickDraw!, Sketchy, and Tu Berlin, along with our generated SketchVCL dataset, show that O3SLM achieves state-of-the-art performance, substantially outperforming existing LVLMs in sketch comprehension and reasoning.

Chimera: Accurate retrosynthesis prediction by ensembling models with diverse inductive biases

Planning and conducting chemical syntheses remains a major bottleneck in the discovery of functional small molecules, and prevents fully leveraging generative AI for molecular inverse design. While early work has shown that ML-based retrosynthesis models can predict reasonable routes, their low accuracy for less frequent, yet important reactions has been pointed out. As multi-step search algorithms are limited to reactions suggested by the underlying model, the applicability of those tools is inherently constrained by the accuracy of retrosynthesis prediction. Inspired by how chemists use different strategies to ideate reactions, we propose Chimera: a framework for building highly accurate reaction models that combine predictions from diverse sources with complementary inductive biases using a learning-based ensembling strategy. We instantiate the framework with two newly developed models, which already by themselves achieve state of the art in their categories. Through experiments across several orders of magnitude in data scale and time-splits, we show Chimera outperforms all major models by a large margin, owing both to the good individual performance of its constituents, but also to the scalability of our ensembling strategy. Moreover, we find that PhD-level organic chemists prefer predictions from Chimera over baselines in terms of quality. Finally, we transfer the largest-scale checkpoint to an internal dataset from a major pharmaceutical company, showing robust generalization under distribution shift. With the new dimension that our framework unlocks, we anticipate further acceleration in the development of even more accurate models.

A PAC Approach to Application-Specific Algorithm Selection

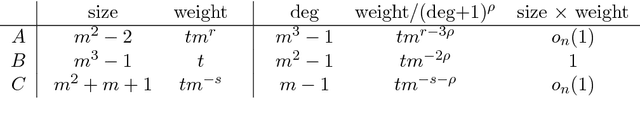
The best algorithm for a computational problem generally depends on the "relevant inputs," a concept that depends on the application domain and often defies formal articulation. While there is a large literature on empirical approaches to selecting the best algorithm for a given application domain, there has been surprisingly little theoretical analysis of the problem. This paper adapts concepts from statistical and online learning theory to reason about application-specific algorithm selection. Our models capture several state-of-the-art empirical and theoretical approaches to the problem, ranging from self-improving algorithms to empirical performance models, and our results identify conditions under which these approaches are guaranteed to perform well. We present one framework that models algorithm selection as a statistical learning problem, and our work here shows that dimension notions from statistical learning theory, historically used to measure the complexity of classes of binary- and real-valued functions, are relevant in a much broader algorithmic context. We also study the online version of the algorithm selection problem, and give possibility and impossibility results for the existence of no-regret learning algorithms.