Renxian Zhang
On Orderings of Probability Vectors and Unsupervised Performance Estimation
Jun 16, 2023



Abstract:Unsupervised performance estimation, or evaluating how well models perform on unlabeled data is a difficult task. Recently, a method was proposed by Garg et al. [2022] which performs much better than previous methods. Their method relies on having a score function, satisfying certain properties, to map probability vectors outputted by the classifier to the reals, but it is an open problem which score function is best. We explore this problem by first showing that their method fundamentally relies on the ordering induced by this score function. Thus, under monotone transformations of score functions, their method yields the same estimate. Next, we show that in the binary classification setting, nearly all common score functions - the $L^\infty$ norm; the $L^2$ norm; negative entropy; and the $L^2$, $L^1$, and Jensen-Shannon distances to the uniform vector - all induce the same ordering over probability vectors. However, this does not hold for higher dimensional settings. We conduct numerous experiments on well-known NLP data sets and rigorously explore the performance of different score functions. We conclude that the $L^\infty$ norm is the most appropriate.
Detecting "Smart" Spammers On Social Network: A Topic Model Approach
Jun 09, 2016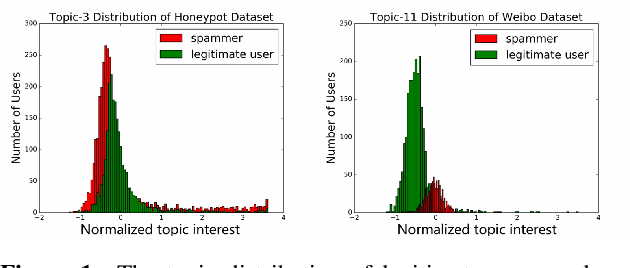
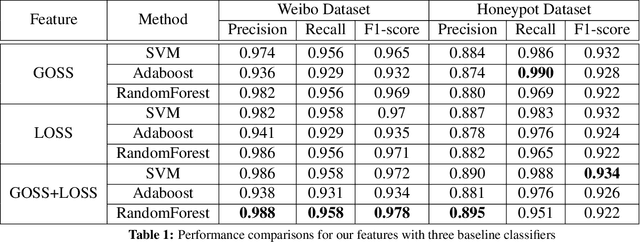
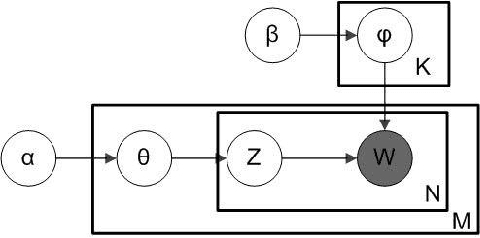
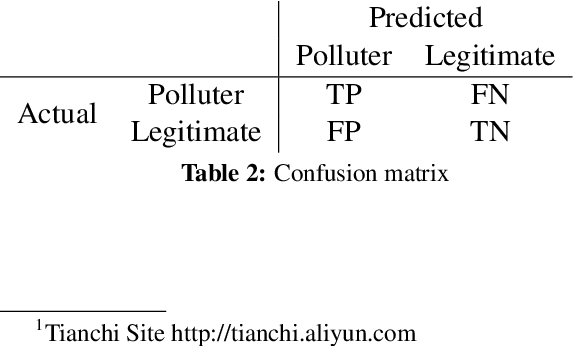
Abstract:Spammer detection on social network is a challenging problem. The rigid anti-spam rules have resulted in emergence of "smart" spammers. They resemble legitimate users who are difficult to identify. In this paper, we present a novel spammer classification approach based on Latent Dirichlet Allocation(LDA), a topic model. Our approach extracts both the local and the global information of topic distribution patterns, which capture the essence of spamming. Tested on one benchmark dataset and one self-collected dataset, our proposed method outperforms other state-of-the-art methods in terms of averaged F1-score.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge