Long-Term Fairness with Unknown Dynamics

While machine learning can myopically reinforce social inequalities, it may also be used to dynamically seek equitable outcomes. In this paper, we formalize long-term fairness in the context of online reinforcement learning. This formulation can accommodate dynamical control objectives, such as driving equity inherent in the state of a population, that cannot be incorporated into static formulations of fairness. We demonstrate that this framing allows an algorithm to adapt to unknown dynamics by sacrificing short-term incentives to drive a classifier-population system towards more desirable equilibria. For the proposed setting, we develop an algorithm that adapts recent work in online learning. We prove that this algorithm achieves simultaneous probabilistic bounds on cumulative loss and cumulative violations of fairness (as statistical regularities between demographic groups). We compare our proposed algorithm to the repeated retraining of myopic classifiers, as a baseline, and to a deep reinforcement learning algorithm that lacks safety guarantees. Our experiments model human populations according to evolutionary game theory and integrate real-world datasets.

Conjugate Natural Selection

We prove that natural gradient descent, with respect to the parameters of a machine learning policy, admits a conjugate dynamical description consistent with evolution by natural selection. We characterize these conjugate dynamics as a locally optimal fit to the continuous-time replicator dynamics, and show that the Price equation applies to equivalence classes of functions belonging to a Hilbert space generated by the policy's architecture and parameters. We posit that "conjugate natural selection" intuitively explains the empirical effectiveness of natural gradient descent, while developing a useful analytic approach to the dynamics of machine learning.

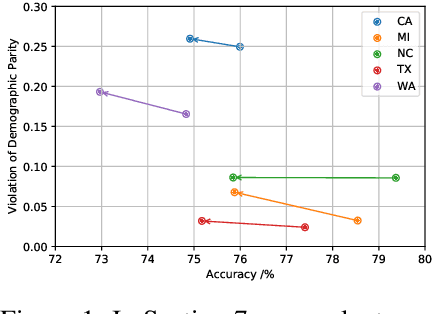
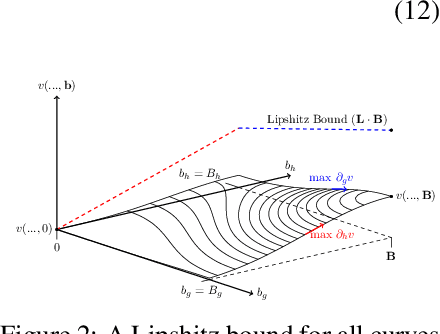
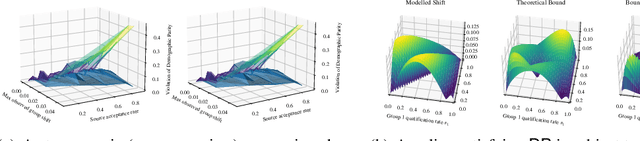
Fairness Transferability Subject to Bounded Distribution Shift

Given an algorithmic predictor that is "fair" on some source distribution, will it still be fair on an unknown target distribution that differs from the source within some bound? In this paper, we study the transferability of statistical group fairness for machine learning predictors (i.e., classifiers or regressors) subject to bounded distribution shift, a phenomenon frequently caused by user adaptation to a deployed model or a dynamic environment. Herein, we develop a bound characterizing such transferability, flagging potentially inappropriate deployments of machine learning for socially consequential tasks. We first develop a framework for bounding violations of statistical fairness subject to distribution shift, formulating a generic upper bound for transferred fairness violation as our primary result. We then develop bounds for specific worked examples, adopting two commonly used fairness definitions (i.e., demographic parity and equalized odds) for two classes of distribution shift (i.e., covariate shift and label shift). Finally, we compare our theoretical bounds to deterministic models of distribution shift as well as real-world data.

Unintended Selection: Persistent Qualification Rate Disparities and Interventions

Realistically -- and equitably -- modeling the dynamics of group-level disparities in machine learning remains an open problem. In particular, we desire models that do not suppose inherent differences between artificial groups of people -- but rather endogenize disparities by appeal to unequal initial conditions of insular subpopulations. In this paper, agents each have a real-valued feature $X$ (e.g., credit score) informed by a "true" binary label $Y$ representing qualification (e.g., for a loan). Each agent alternately (1) receives a binary classification label $\hat{Y}$ (e.g., loan approval) from a Bayes-optimal machine learning classifier observing $X$ and (2) may update their qualification $Y$ by imitating successful strategies (e.g., seek a raise) within an isolated group $G$ of agents to which they belong. We consider the disparity of qualification rates $\Pr(Y=1)$ between different groups and how this disparity changes subject to a sequence of Bayes-optimal classifiers repeatedly retrained on the global population. We model the evolving qualification rates of each subpopulation (group) using the replicator equation, which derives from a class of imitation processes. We show that differences in qualification rates between subpopulations can persist indefinitely for a set of non-trivial equilibrium states due to uniformed classifier deployments, even when groups are identical in all aspects except initial qualification densities. We next simulate the effects of commonly proposed fairness interventions on this dynamical system along with a new feedback control mechanism capable of permanently eliminating group-level qualification rate disparities. We conclude by discussing the limitations of our model and findings and by outlining potential future work.