LoRA vs Full Fine-tuning: An Illusion of Equivalence

Fine-tuning is a crucial paradigm for adapting pre-trained large language models to downstream tasks. Recently, methods like Low-Rank Adaptation (LoRA) have been shown to match the performance of fully fine-tuned models on various tasks with an extreme reduction in the number of trainable parameters. Even in settings where both methods learn similarly accurate models, \emph{are their learned solutions really equivalent?} We study how different fine-tuning methods change pre-trained models by analyzing the model's weight matrices through the lens of their spectral properties. We find that full fine-tuning and LoRA yield weight matrices whose singular value decompositions exhibit very different structure; moreover, the fine-tuned models themselves show distinct generalization behaviors when tested outside the adaptation task's distribution. More specifically, we first show that the weight matrices trained with LoRA have new, high-ranking singular vectors, which we call \emph{intruder dimensions}. Intruder dimensions do not appear during full fine-tuning. Second, we show that LoRA models with intruder dimensions, despite achieving similar performance to full fine-tuning on the target task, become worse models of the pre-training distribution and adapt less robustly to multiple tasks sequentially. Higher-rank, rank-stabilized LoRA models closely mirror full fine-tuning, even when performing on par with lower-rank LoRA models on the same tasks. These results suggest that models updated with LoRA and full fine-tuning access different parts of parameter space, even when they perform equally on the fine-tuned distribution. We conclude by examining why intruder dimensions appear in LoRA fine-tuned models, why they are undesirable, and how their effects can be minimized.

A Dataset and Benchmark for Automatically Answering and Generating Machine Learning Final Exams

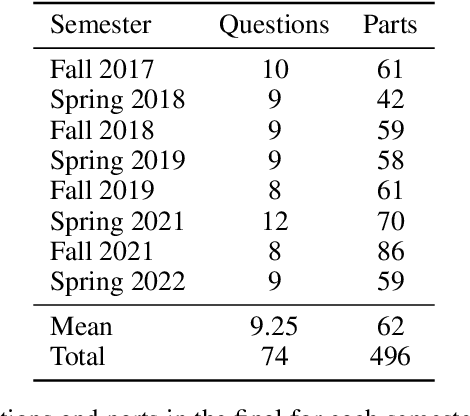
Can a machine learn machine learning? We propose to answer this question using the same criteria we use to answer a similar question: can a human learn machine learning? We automatically answer MIT final exams in Introduction to Machine Learning at a human level. The course is a large undergraduate class with around five hundred students each semester. Recently, program synthesis and few-shot learning solved university-level problem set questions in mathematics and STEM courses at a human level. In this work, we solve questions from final exams that differ from problem sets in several ways: the questions are longer, have multiple parts, are more complicated, and span a broader set of topics. We provide a new dataset and benchmark of questions from eight MIT Introduction to Machine Learning final exams between Fall 2017 and Spring 2022 and provide code for automatically answering these questions and generating new questions. We perform ablation studies comparing zero-shot learning with few-shot learning, chain-of-thought prompting, GPT-3 pre-trained on text and Codex fine-tuned on code on a range of machine learning topics and find that few-shot learning methods perform best. We make our data and code publicly available for the machine learning community.