Double-Linear Thompson Sampling for Context-Attentive Bandits

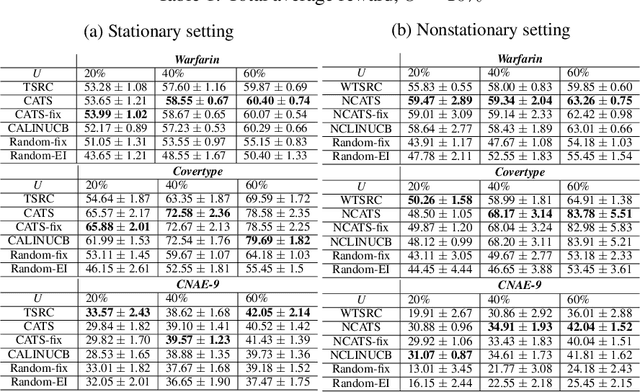
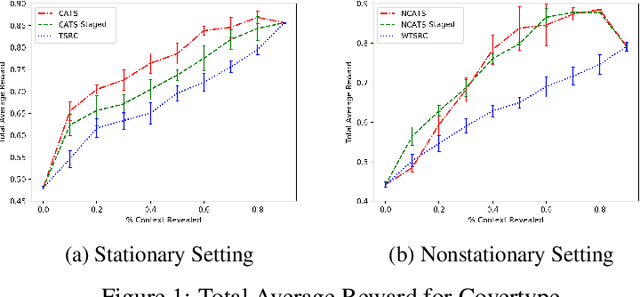
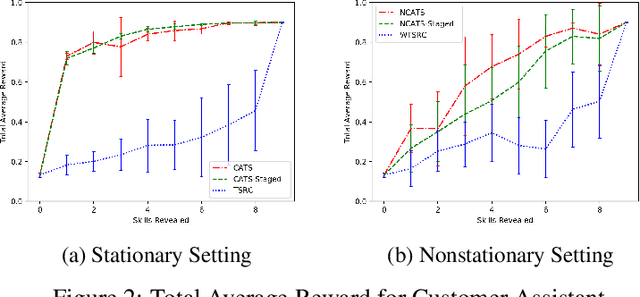
In this paper, we analyze and extend an online learning framework known as Context-Attentive Bandit, motivated by various practical applications, from medical diagnosis to dialog systems, where due to observation costs only a small subset of a potentially large number of context variables can be observed at each iteration;however, the agent has a freedom to choose which variables to observe. We derive a novel algorithm, called Context-Attentive Thompson Sampling (CATS), which builds upon the Linear Thompson Sampling approach, adapting it to Context-Attentive Bandit setting. We provide a theoretical regret analysis and an extensive empirical evaluation demonstrating advantages of the proposed approach over several baseline methods on a variety of real-life datasets

Decentralized Exploration in Multi-Armed Bandits

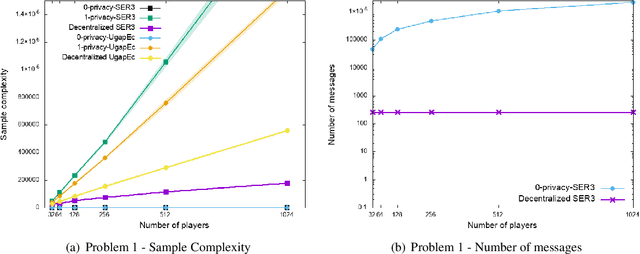
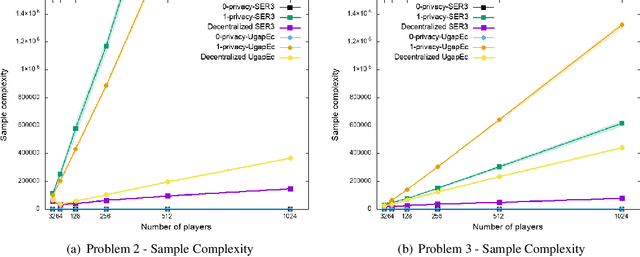
We consider the \textit {decentralized exploration problem}: a set of players collaborate to identify the best arm by asynchronously interacting with the same stochastic environment. The objective is to insure privacy in the best arm identification problem between asynchronous, collaborative, and thrifty players. In the context of a digital service, we advocate that this decentralized approach allows a good balance between the interests of users and those of service providers: the providers optimize their services, while protecting the privacy of the users and saving resources. We define the privacy level as the amount of information an adversary could infer by intercepting the messages concerning a single user. We provide a generic algorithm {\sc Decentralized Elimination}, which uses any best arm identification algorithm as a subroutine. We prove that this algorithm insures privacy, with a low communication cost, and that in comparison to the lower bound of the best arm identification problem, its sample complexity suffers from a penalty depending on the inverse of the probability of the most frequent players. Then, thanks to the genericity of the approach, we extend the proposed algorithm to the non-stationary bandits. Finally, experiments illustrate and complete the analysis.

Network of Bandits insure Privacy of end-users

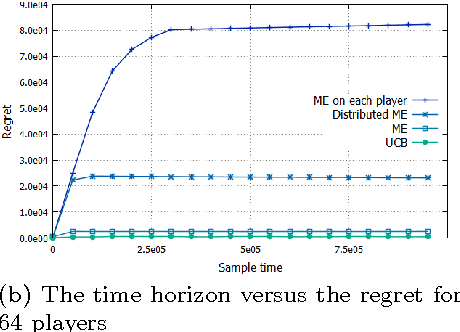
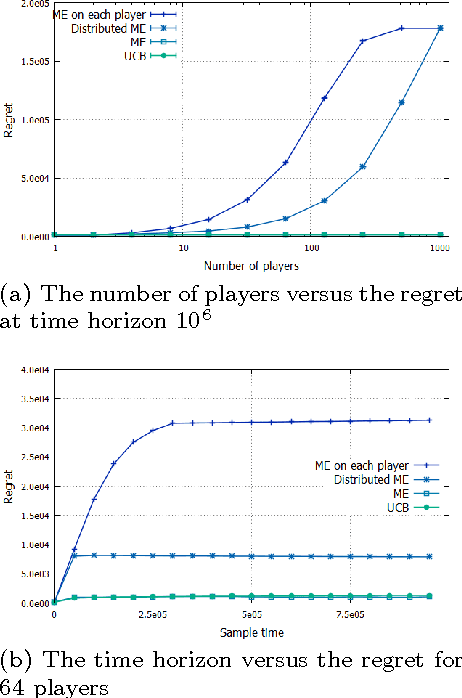
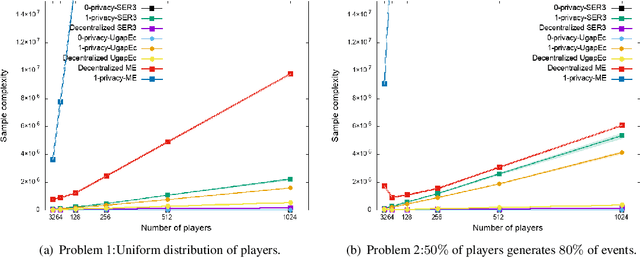
In order to distribute the best arm identification task as close as possible to the user's devices, on the edge of the Radio Access Network, we propose a new problem setting, where distributed players collaborate to find the best arm. This architecture guarantees privacy to end-users since no events are stored. The only thing that can be observed by an adversary through the core network is aggregated information across users. We provide a first algorithm, Distributed Median Elimination, which is optimal in term of number of transmitted bits and near optimal in term of speed-up factor with respect to an optimal algorithm run independently on each player. In practice, this first algorithm cannot handle the trade-off between the communication cost and the speed-up factor, and requires some knowledge about the distribution of players. Extended Distributed Median Elimination overcomes these limitations, by playing in parallel different instances of Distributed Median Elimination and selecting the best one. Experiments illustrate and complete the analysis. According to the analysis, in comparison to Median Elimination performed on each player, the proposed algorithm shows significant practical improvements.

Random Forest for the Contextual Bandit Problem - extended version

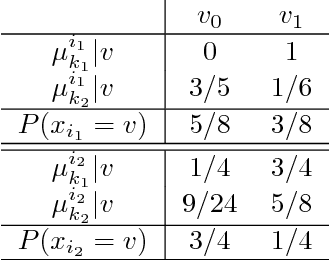
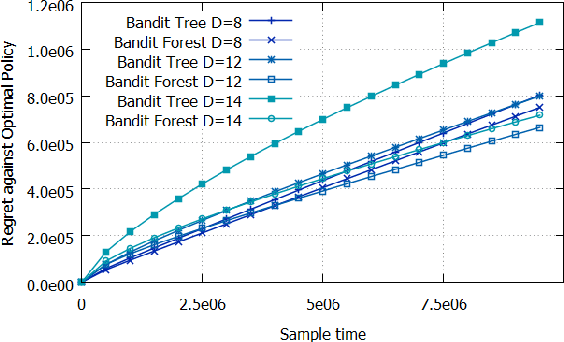
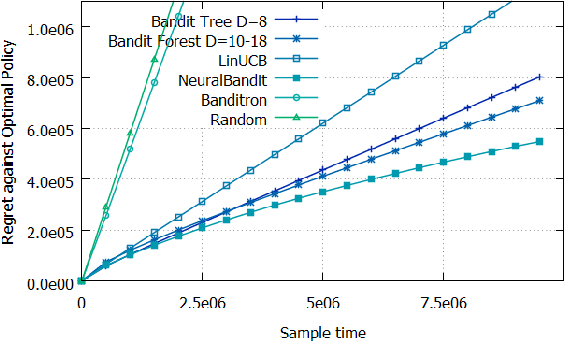
To address the contextual bandit problem, we propose an online random forest algorithm. The analysis of the proposed algorithm is based on the sample complexity needed to find the optimal decision stump. Then, the decision stumps are assembled in a random collection of decision trees, Bandit Forest. We show that the proposed algorithm is optimal up to logarithmic factors. The dependence of the sample complexity upon the number of contextual variables is logarithmic. The computational cost of the proposed algorithm with respect to the time horizon is linear. These analytical results allow the proposed algorithm to be efficient in real applications, where the number of events to process is huge, and where we expect that some contextual variables, chosen from a large set, have potentially non- linear dependencies with the rewards. In the experiments done to illustrate the theoretical analysis, Bandit Forest obtain promising results in comparison with state-of-the-art algorithms.

Random Shuffling and Resets for the Non-stationary Stochastic Bandit Problem

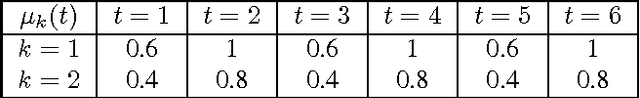
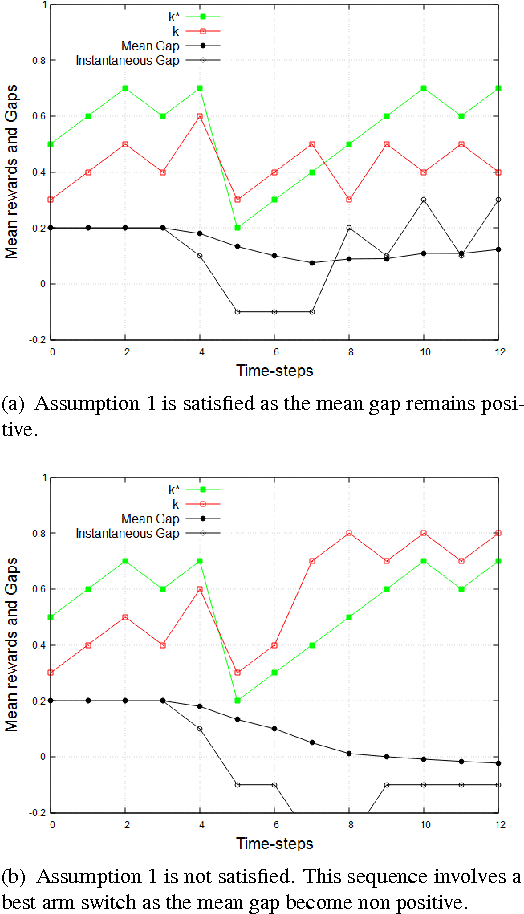
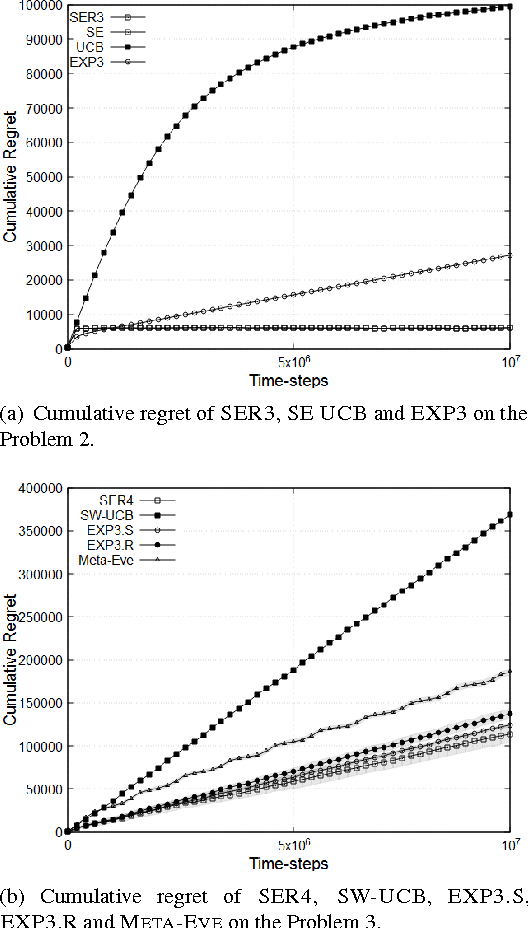
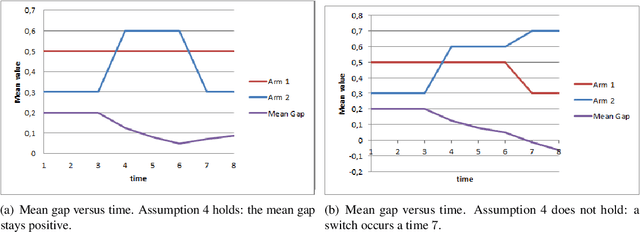
We consider a non-stationary formulation of the stochastic multi-armed bandit where the rewards are no longer assumed to be identically distributed. For the best-arm identification task, we introduce a version of Successive Elimination based on random shuffling of the $K$ arms. We prove that under a novel and mild assumption on the mean gap $\Delta$, this simple but powerful modification achieves the same guarantees in term of sample complexity and cumulative regret than its original version, but in a much wider class of problems, as it is not anymore constrained to stationary distributions. We also show that the original {\sc Successive Elimination} fails to have controlled regret in this more general scenario, thus showing the benefit of shuffling. We then remove our mild assumption and adapt the algorithm to the best-arm identification task with switching arms. We adapt the definition of the sample complexity for that case and prove that, against an optimal policy with $N-1$ switches of the optimal arm, this new algorithm achieves an expected sample complexity of $O(\Delta^{-2}\sqrt{NK\delta^{-1} \log(K \delta^{-1})})$, where $\delta$ is the probability of failure of the algorithm, and an expected cumulative regret of $O(\Delta^{-1}{\sqrt{NTK \log (TK)}})$ after $T$ time steps.