Random Forest for the Contextual Bandit Problem - extended version
Paper and Code
Sep 15, 2016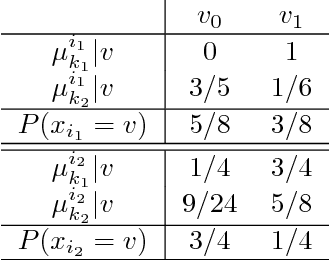
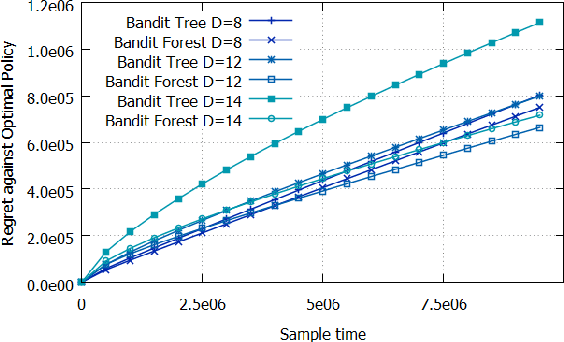
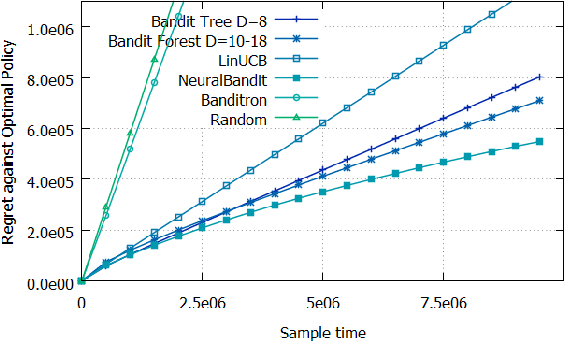

To address the contextual bandit problem, we propose an online random forest algorithm. The analysis of the proposed algorithm is based on the sample complexity needed to find the optimal decision stump. Then, the decision stumps are assembled in a random collection of decision trees, Bandit Forest. We show that the proposed algorithm is optimal up to logarithmic factors. The dependence of the sample complexity upon the number of contextual variables is logarithmic. The computational cost of the proposed algorithm with respect to the time horizon is linear. These analytical results allow the proposed algorithm to be efficient in real applications, where the number of events to process is huge, and where we expect that some contextual variables, chosen from a large set, have potentially non- linear dependencies with the rewards. In the experiments done to illustrate the theoretical analysis, Bandit Forest obtain promising results in comparison with state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge