Random Forest for the Contextual Bandit Problem - extended version

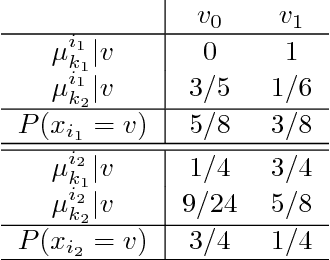
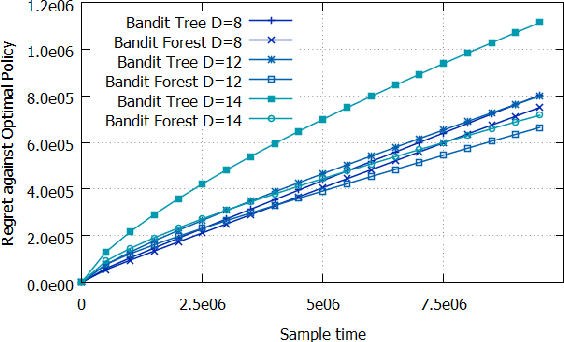
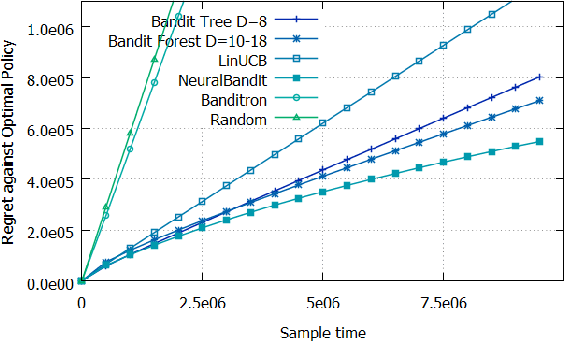
To address the contextual bandit problem, we propose an online random forest algorithm. The analysis of the proposed algorithm is based on the sample complexity needed to find the optimal decision stump. Then, the decision stumps are assembled in a random collection of decision trees, Bandit Forest. We show that the proposed algorithm is optimal up to logarithmic factors. The dependence of the sample complexity upon the number of contextual variables is logarithmic. The computational cost of the proposed algorithm with respect to the time horizon is linear. These analytical results allow the proposed algorithm to be efficient in real applications, where the number of events to process is huge, and where we expect that some contextual variables, chosen from a large set, have potentially non- linear dependencies with the rewards. In the experiments done to illustrate the theoretical analysis, Bandit Forest obtain promising results in comparison with state-of-the-art algorithms.

Random Shuffling and Resets for the Non-stationary Stochastic Bandit Problem

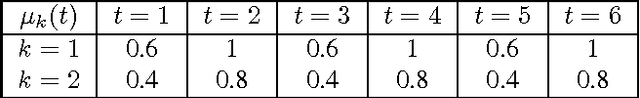
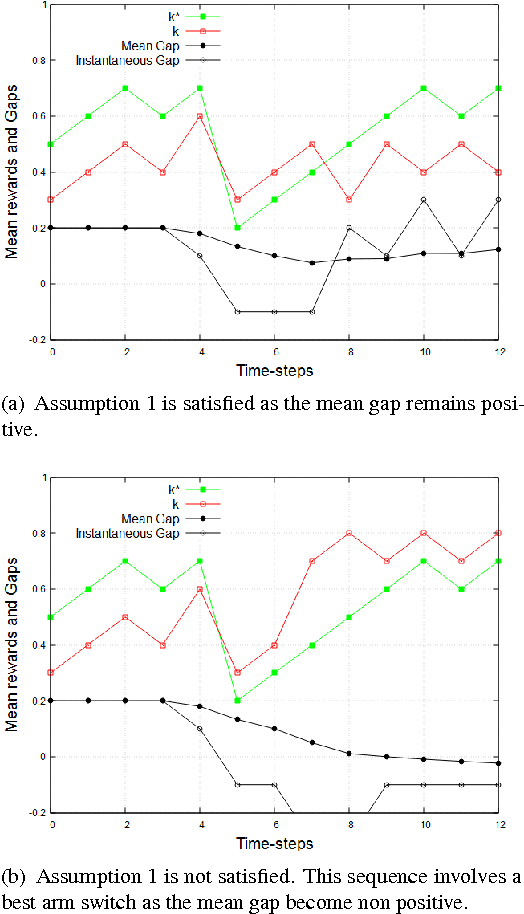
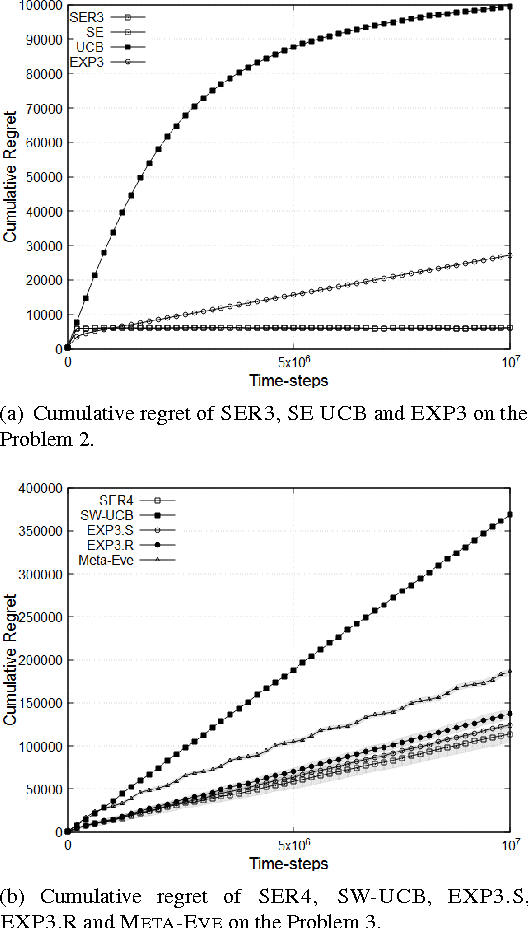
We consider a non-stationary formulation of the stochastic multi-armed bandit where the rewards are no longer assumed to be identically distributed. For the best-arm identification task, we introduce a version of Successive Elimination based on random shuffling of the $K$ arms. We prove that under a novel and mild assumption on the mean gap $\Delta$, this simple but powerful modification achieves the same guarantees in term of sample complexity and cumulative regret than its original version, but in a much wider class of problems, as it is not anymore constrained to stationary distributions. We also show that the original {\sc Successive Elimination} fails to have controlled regret in this more general scenario, thus showing the benefit of shuffling. We then remove our mild assumption and adapt the algorithm to the best-arm identification task with switching arms. We adapt the definition of the sample complexity for that case and prove that, against an optimal policy with $N-1$ switches of the optimal arm, this new algorithm achieves an expected sample complexity of $O(\Delta^{-2}\sqrt{NK\delta^{-1} \log(K \delta^{-1})})$, where $\delta$ is the probability of failure of the algorithm, and an expected cumulative regret of $O(\Delta^{-1}{\sqrt{NTK \log (TK)}})$ after $T$ time steps.

A Neural Networks Committee for the Contextual Bandit Problem

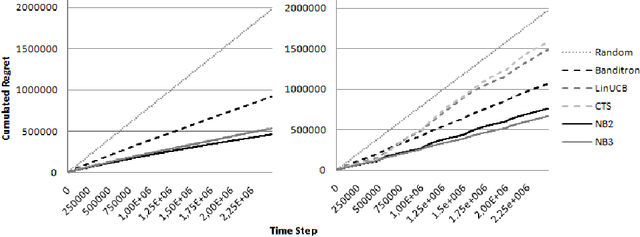
This paper presents a new contextual bandit algorithm, NeuralBandit, which does not need hypothesis on stationarity of contexts and rewards. Several neural networks are trained to modelize the value of rewards knowing the context. Two variants, based on multi-experts approach, are proposed to choose online the parameters of multi-layer perceptrons. The proposed algorithms are successfully tested on a large dataset with and without stationarity of rewards.