Puzzle: Distillation-Based NAS for Inference-Optimized LLMs

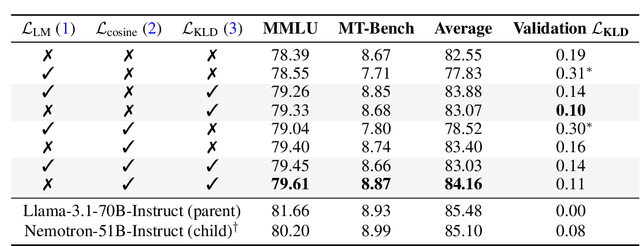
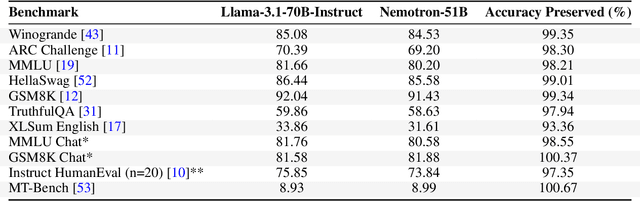
Large language models (LLMs) have demonstrated remarkable capabilities, but their adoption is limited by high computational costs during inference. While increasing parameter counts enhances accuracy, it also widens the gap between state-of-the-art capabilities and practical deployability. We present Puzzle, a framework to accelerate LLM inference on specific hardware while preserving their capabilities. Through an innovative application of neural architecture search (NAS) at an unprecedented scale, Puzzle systematically optimizes models with tens of billions of parameters under hardware constraints. Our approach utilizes blockwise local knowledge distillation (BLD) for parallel architecture exploration and employs mixed-integer programming for precise constraint optimization. We demonstrate the real-world impact of our framework through Llama-3.1-Nemotron-51B-Instruct (Nemotron-51B), a publicly available model derived from Llama-3.1-70B-Instruct. Nemotron-51B achieves a 2.17x inference throughput speedup, fitting on a single NVIDIA H100 GPU while preserving 98.4% of the original model's capabilities. Nemotron-51B currently stands as the most accurate language model capable of inference on a single GPU with large batch sizes. Remarkably, this transformation required just 45B training tokens, compared to over 15T tokens used for the 70B model it was derived from. This establishes a new paradigm where powerful models can be optimized for efficient deployment with only negligible compromise of their capabilities, demonstrating that inference performance, not parameter count alone, should guide model selection. With the release of Nemotron-51B and the presentation of the Puzzle framework, we provide practitioners immediate access to state-of-the-art language modeling capabilities at significantly reduced computational costs.

Temporal support vectors for spiking neuronal networks

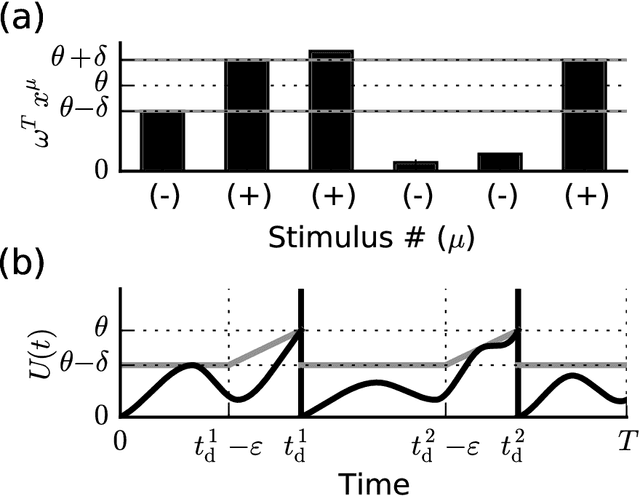
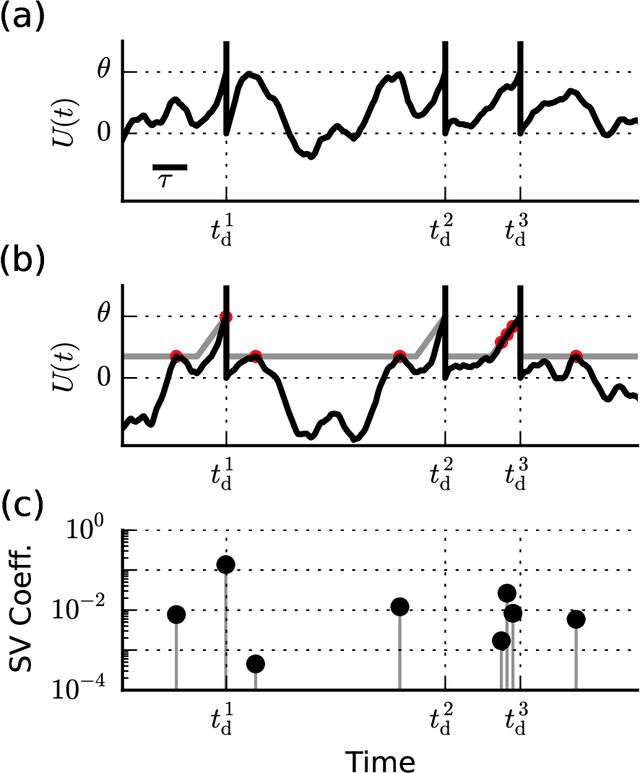
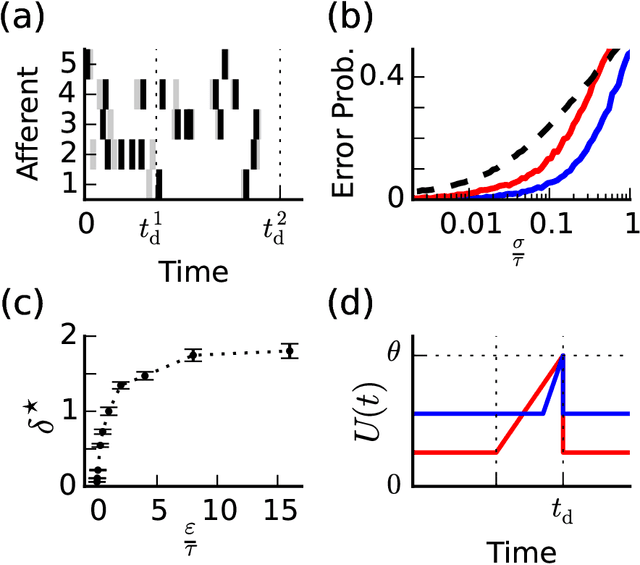
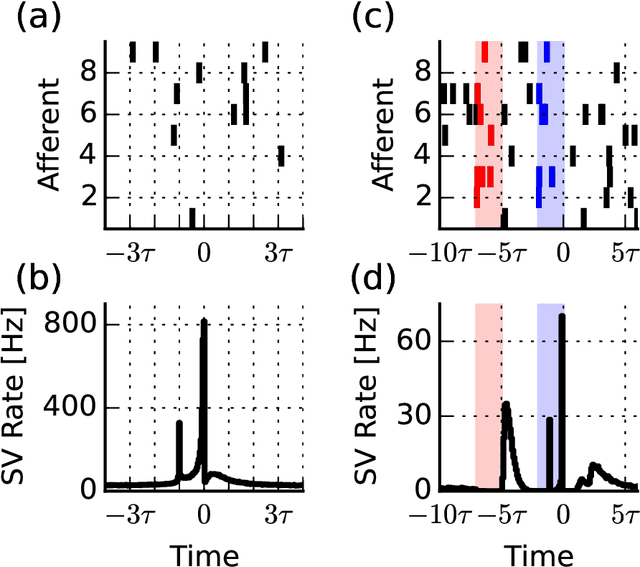
When neural circuits learn to perform a task, it is often the case that there are many sets of synaptic connections that are consistent with the task. However, only a small number of possible solutions are robust to noise in the input and are capable of generalizing their performance of the task to new inputs. Finding such good solutions is an important goal of learning systems in general and neuronal circuits in particular. For systems operating with static inputs and outputs, a well known approach to the problem is the large margin methods such as Support Vector Machines (SVM). By maximizing the distance of the data vectors from the decision surface, these solutions enjoy increased robustness to noise and enhanced generalization abilities. Furthermore, the use of the kernel method enables SVMs to perform classification tasks that require nonlinear decision surfaces. However, for dynamical systems with event based outputs, such as spiking neural networks and other continuous time threshold crossing systems, this optimality criterion is inapplicable due to the strong temporal correlations in their input and output. We introduce a novel extension of the static SVMs - The Temporal Support Vector Machine (T-SVM). The T-SVM finds a solution that maximizes a new construct - the dynamical margin. We show that T-SVM and its kernel extensions generate robust synaptic weight vectors in spiking neurons and enable their learning of tasks that require nonlinear spatial integration of synaptic inputs. We propose T-SVM with nonlinear kernels as a new model of the computational role of the nonlinearities and extensive morphologies of neuronal dendritic trees.

New Heuristics for Parallel and Scalable Bayesian Optimization

Bayesian optimization has emerged as a strong candidate tool for global optimization of functions with expensive evaluation costs. However, due to the dynamic nature of research in Bayesian approaches, and the evolution of computing technology, using Bayesian optimization in a parallel computing environment remains a challenge for the non-expert. In this report, I review the state-of-the-art in parallel and scalable Bayesian optimization methods. In addition, I propose practical ways to avoid a few of the pitfalls of Bayesian optimization, such as oversampling of edge parameters and over-exploitation of high performance parameters. Finally, I provide relatively simple, heuristic algorithms, along with their open source software implementations, that can be immediately and easily deployed in any computing environment.

Balanced Excitation and Inhibition are Required for High-Capacity, Noise-Robust Neuronal Selectivity

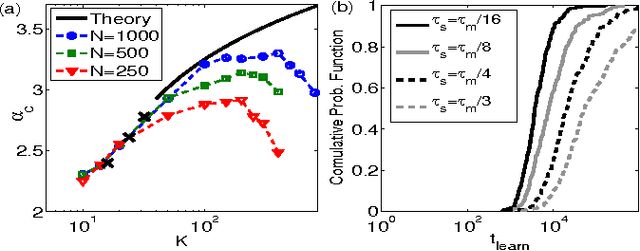
Neurons and networks in the cerebral cortex must operate reliably despite multiple sources of noise. To evaluate the impact of both input and output noise, we determine the robustness of single-neuron stimulus selective responses, as well as the robustness of attractor states of networks of neurons performing memory tasks. We find that robustness to output noise requires synaptic connections to be in a balanced regime in which excitation and inhibition are strong and largely cancel each other. We evaluate the conditions required for this regime to exist and determine the properties of networks operating within it. A plausible synaptic plasticity rule for learning that balances weight configurations is presented. Our theory predicts an optimal ratio of the number of excitatory and inhibitory synapses for maximizing the encoding capacity of balanced networks for a given statistics of afferent activations. Previous work has shown that balanced networks amplify spatio-temporal variability and account for observed asynchronous irregular states. Here we present a novel type of balanced network that amplifies small changes in the impinging signals, and emerges automatically from learning to perform neuronal and network functions robustly.

Theory of spike timing based neural classifiers

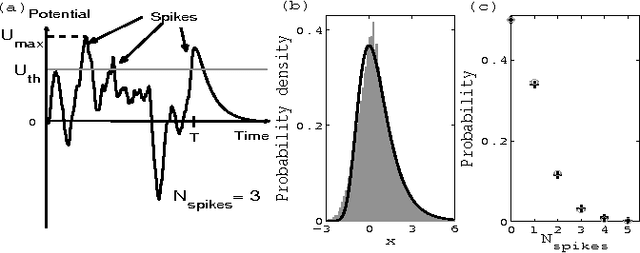
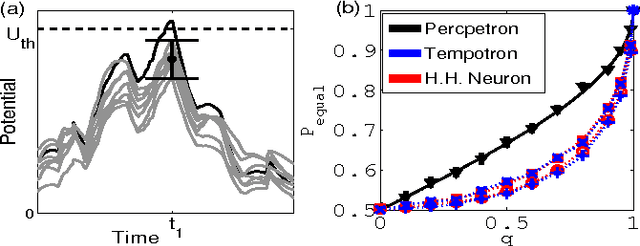
We study the computational capacity of a model neuron, the Tempotron, which classifies sequences of spikes by linear-threshold operations. We use statistical mechanics and extreme value theory to derive the capacity of the system in random classification tasks. In contrast to its static analog, the Perceptron, the Tempotron's solutions space consists of a large number of small clusters of weight vectors. The capacity of the system per synapse is finite in the large size limit and weakly diverges with the stimulus duration relative to the membrane and synaptic time constants.