Temporal support vectors for spiking neuronal networks
Paper and Code
May 28, 2022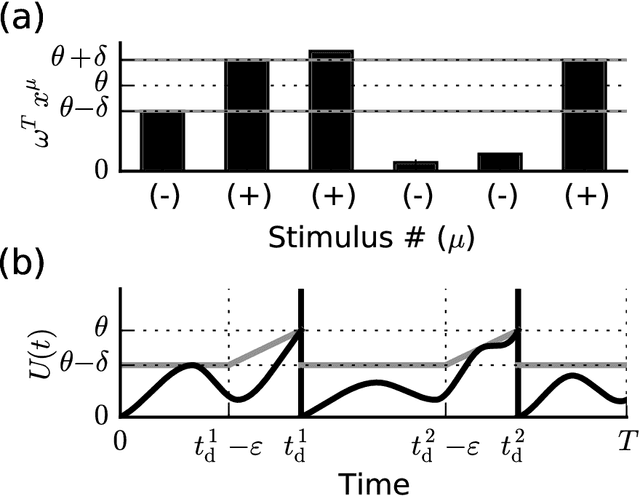
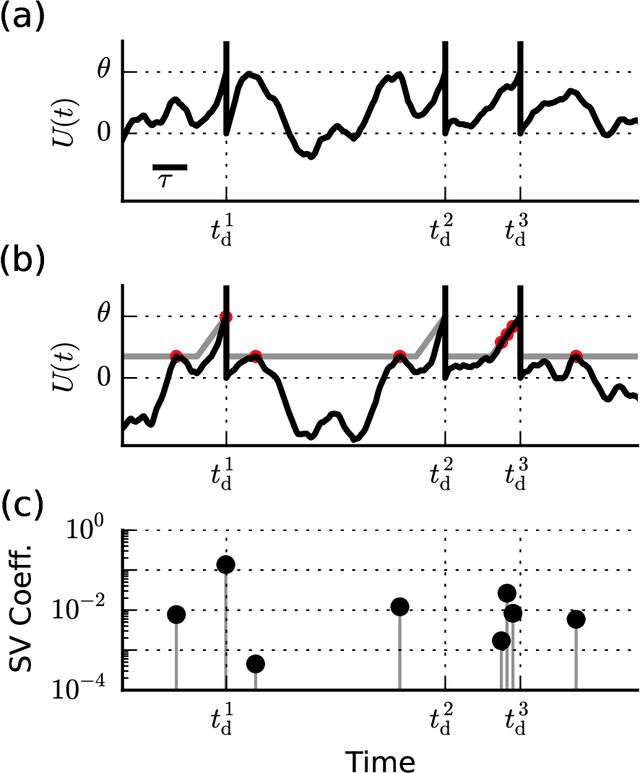
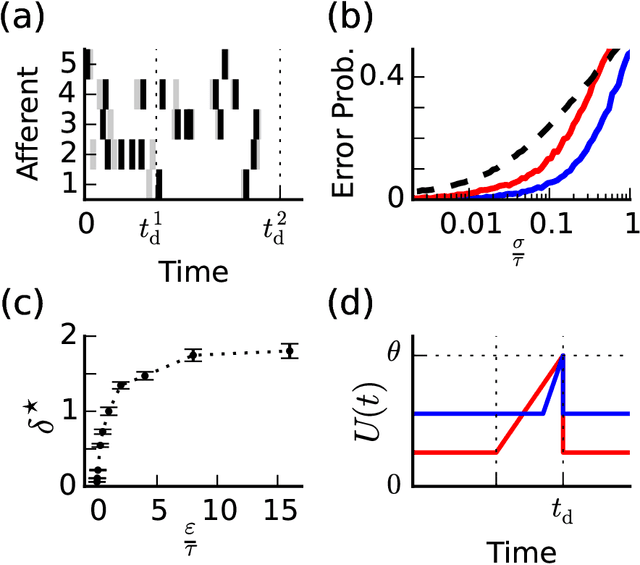
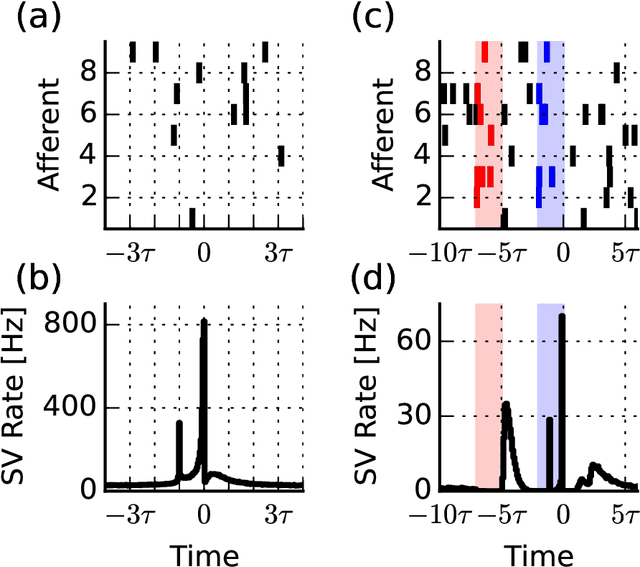
When neural circuits learn to perform a task, it is often the case that there are many sets of synaptic connections that are consistent with the task. However, only a small number of possible solutions are robust to noise in the input and are capable of generalizing their performance of the task to new inputs. Finding such good solutions is an important goal of learning systems in general and neuronal circuits in particular. For systems operating with static inputs and outputs, a well known approach to the problem is the large margin methods such as Support Vector Machines (SVM). By maximizing the distance of the data vectors from the decision surface, these solutions enjoy increased robustness to noise and enhanced generalization abilities. Furthermore, the use of the kernel method enables SVMs to perform classification tasks that require nonlinear decision surfaces. However, for dynamical systems with event based outputs, such as spiking neural networks and other continuous time threshold crossing systems, this optimality criterion is inapplicable due to the strong temporal correlations in their input and output. We introduce a novel extension of the static SVMs - The Temporal Support Vector Machine (T-SVM). The T-SVM finds a solution that maximizes a new construct - the dynamical margin. We show that T-SVM and its kernel extensions generate robust synaptic weight vectors in spiking neurons and enable their learning of tasks that require nonlinear spatial integration of synaptic inputs. We propose T-SVM with nonlinear kernels as a new model of the computational role of the nonlinearities and extensive morphologies of neuronal dendritic trees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge