Disentangling representations in Restricted Boltzmann Machines without adversaries

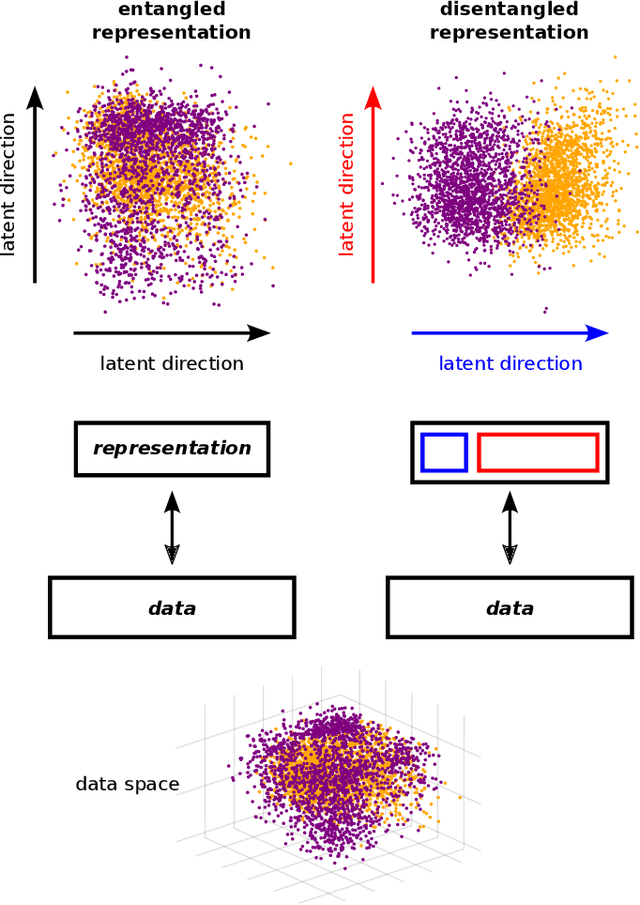
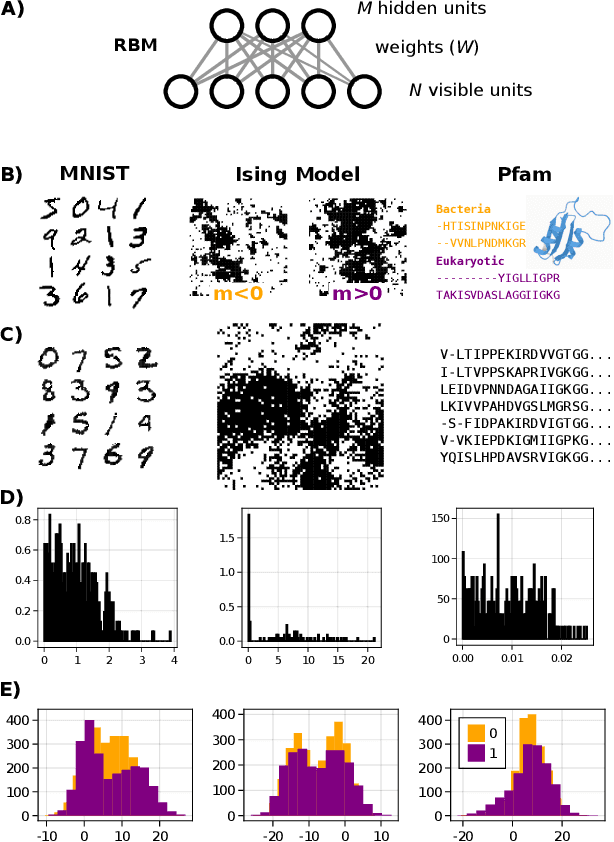
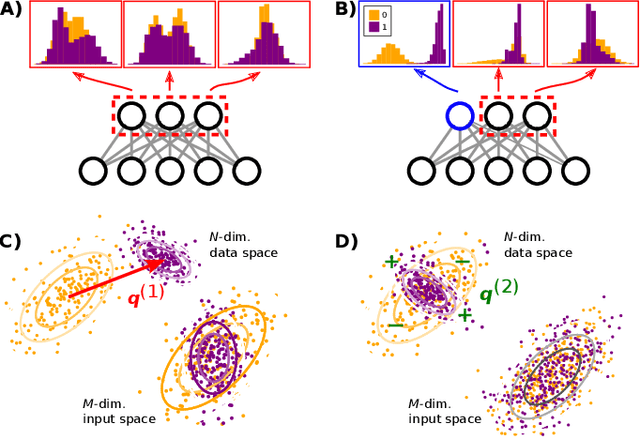
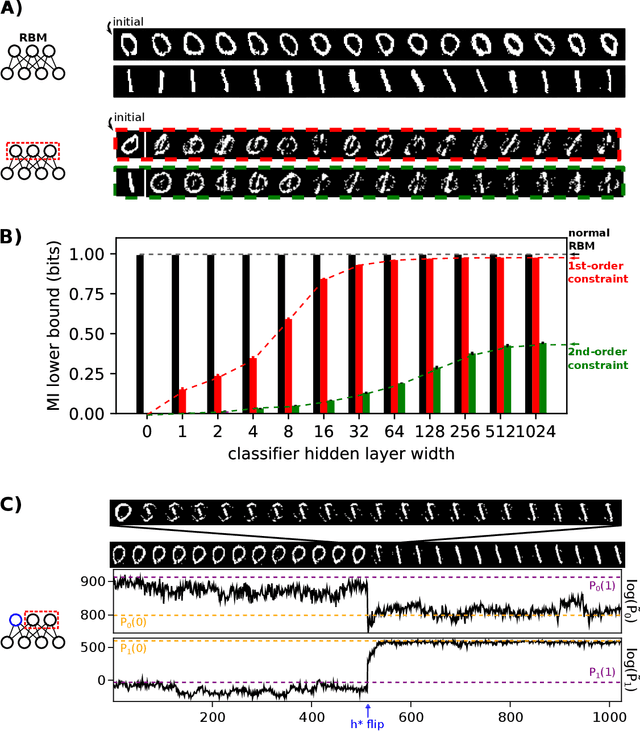
A goal of unsupervised machine learning is to disentangle representations of complex high-dimensional data, allowing for interpreting the significant latent factors of variation in the data as well as for manipulating them to generate new data with desirable features. These methods often rely on an adversarial scheme, in which representations are tuned to avoid discriminators from being able to reconstruct specific data information (labels). We propose a simple, effective way of disentangling representations without any need to train adversarial discriminators, and apply our approach to Restricted Boltzmann Machines (RBM), one of the simplest representation-based generative models. Our approach relies on the introduction of adequate constraints on the weights during training, which allows us to concentrate information about labels on a small subset of latent variables. The effectiveness of the approach is illustrated on the MNIST dataset, the two-dimensional Ising model, and taxonomy of protein families. In addition, we show how our framework allows for computing the cost, in terms of log-likelihood of the data, associated to the disentanglement of their representations.

'Place-cell' emergence and learning of invariant data with restricted Boltzmann machines: breaking and dynamical restoration of continuous symmetries in the weight space

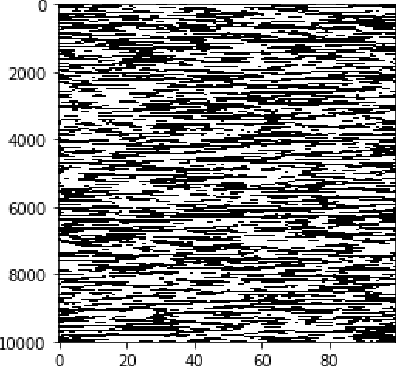
Distributions of data or sensory stimuli often enjoy underlying invariances. How and to what extent those symmetries are captured by unsupervised learning methods is a relevant question in machine learning and in computational neuroscience. We study here, through a combination of numerical and analytical tools, the learning dynamics of Restricted Boltzmann Machines (RBM), a neural network paradigm for representation learning. As learning proceeds from a random configuration of the network weights, we show the existence of, and characterize a symmetry-breaking phenomenon, in which the latent variables acquire receptive fields focusing on limited parts of the invariant manifold supporting the data. The symmetry is restored at large learning times through the diffusion of the receptive field over the invariant manifold; hence, the RBM effectively spans a continuous attractor in the space of network weights. This symmetry-breaking phenomenon takes place only if the amount of data available for training exceeds some critical value, depending on the network size and the intensity of symmetry-induced correlations in the data; below this 'retarded-learning' threshold, the network weights are essentially noisy and overfit the data.

High-Dimensional Inference with the generalized Hopfield Model: Principal Component Analysis and Corrections

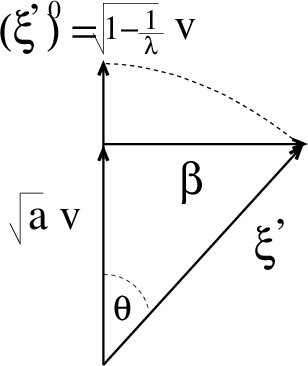
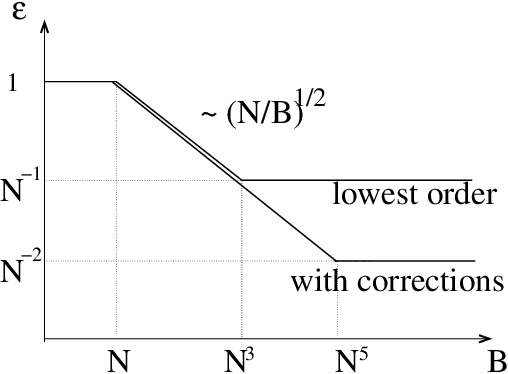
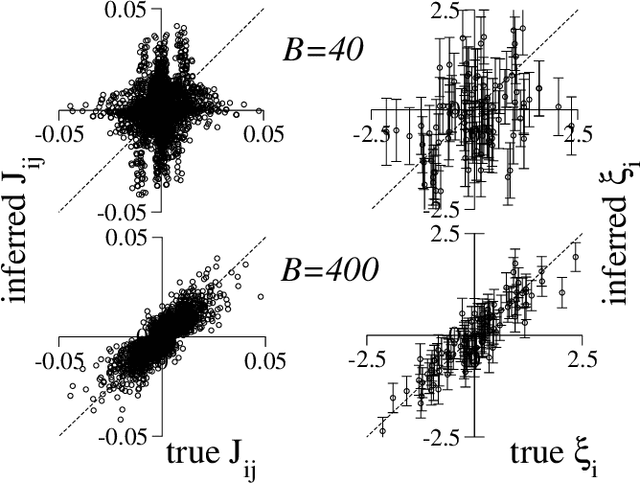
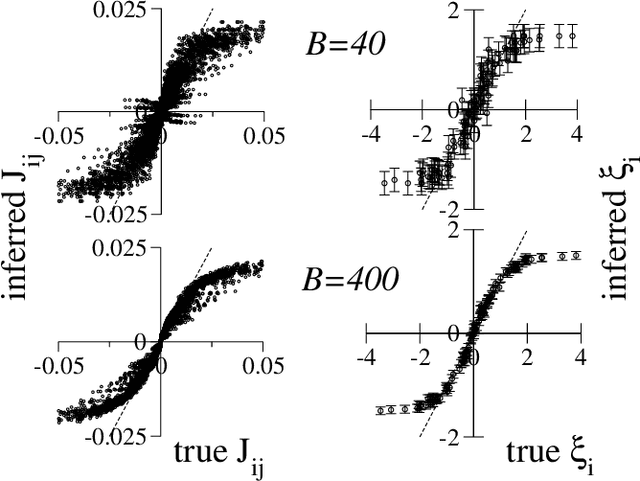
We consider the problem of inferring the interactions between a set of N binary variables from the knowledge of their frequencies and pairwise correlations. The inference framework is based on the Hopfield model, a special case of the Ising model where the interaction matrix is defined through a set of patterns in the variable space, and is of rank much smaller than N. We show that Maximum Lik elihood inference is deeply related to Principal Component Analysis when the amp litude of the pattern components, xi, is negligible compared to N^1/2. Using techniques from statistical mechanics, we calculate the corrections to the patterns to the first order in xi/N^1/2. We stress that it is important to generalize the Hopfield model and include both attractive and repulsive patterns, to correctly infer networks with sparse and strong interactions. We present a simple geometrical criterion to decide how many attractive and repulsive patterns should be considered as a function of the sampling noise. We moreover discuss how many sampled configurations are required for a good inference, as a function of the system size, N and of the amplitude, xi. The inference approach is illustrated on synthetic and biological data.

Fast Inference of Interactions in Assemblies of Stochastic Integrate-and-Fire Neurons from Spike Recordings

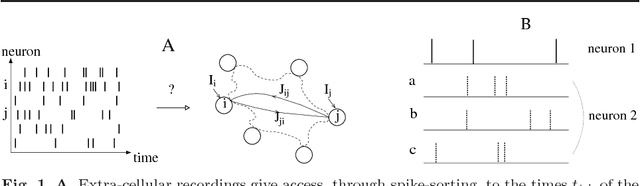
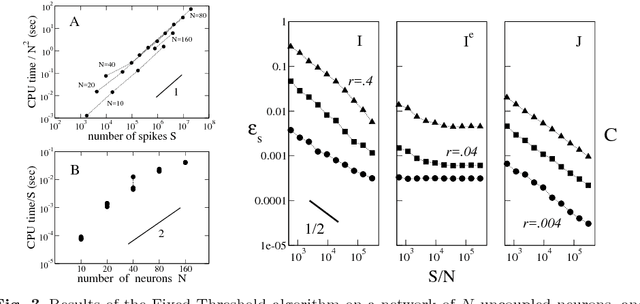
We present two Bayesian procedures to infer the interactions and external currents in an assembly of stochastic integrate-and-fire neurons from the recording of their spiking activity. The first procedure is based on the exact calculation of the most likely time courses of the neuron membrane potentials conditioned by the recorded spikes, and is exact for a vanishing noise variance and for an instantaneous synaptic integration. The second procedure takes into account the presence of fluctuations around the most likely time courses of the potentials, and can deal with moderate noise levels. The running time of both procedures is proportional to the number S of spikes multiplied by the squared number N of neurons. The algorithms are validated on synthetic data generated by networks with known couplings and currents. We also reanalyze previously published recordings of the activity of the salamander retina (including from 32 to 40 neurons, and from 65,000 to 170,000 spikes). We study the dependence of the inferred interactions on the membrane leaking time; the differences and similarities with the classical cross-correlation analysis are discussed.

Theory of spike timing based neural classifiers

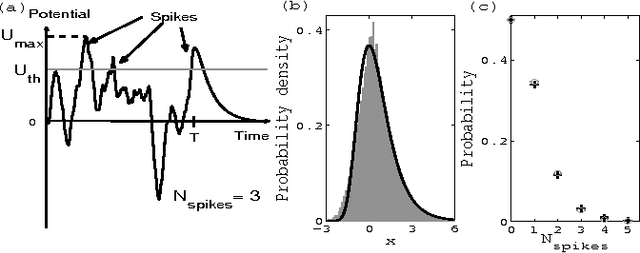
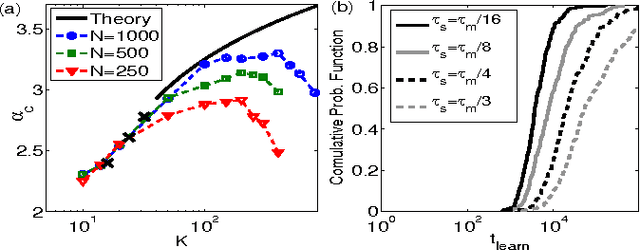
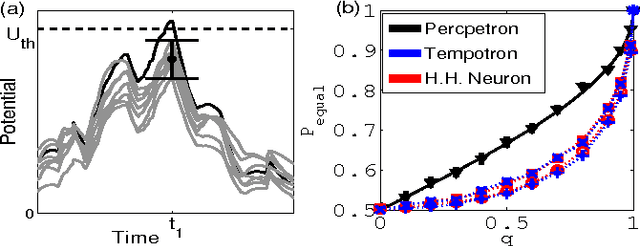
We study the computational capacity of a model neuron, the Tempotron, which classifies sequences of spikes by linear-threshold operations. We use statistical mechanics and extreme value theory to derive the capacity of the system in random classification tasks. In contrast to its static analog, the Perceptron, the Tempotron's solutions space consists of a large number of small clusters of weight vectors. The capacity of the system per synapse is finite in the large size limit and weakly diverges with the stimulus duration relative to the membrane and synaptic time constants.