Moshir Harsh
LPENS, PSL
'Place-cell' emergence and learning of invariant data with restricted Boltzmann machines: breaking and dynamical restoration of continuous symmetries in the weight space
Dec 30, 2019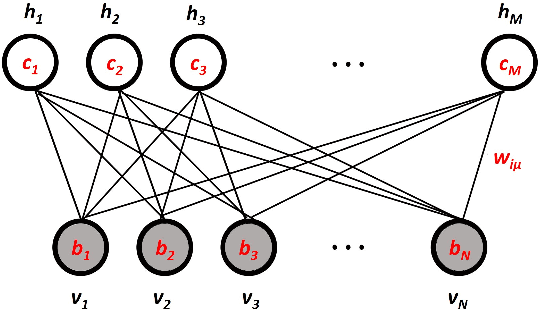


Abstract:Distributions of data or sensory stimuli often enjoy underlying invariances. How and to what extent those symmetries are captured by unsupervised learning methods is a relevant question in machine learning and in computational neuroscience. We study here, through a combination of numerical and analytical tools, the learning dynamics of Restricted Boltzmann Machines (RBM), a neural network paradigm for representation learning. As learning proceeds from a random configuration of the network weights, we show the existence of, and characterize a symmetry-breaking phenomenon, in which the latent variables acquire receptive fields focusing on limited parts of the invariant manifold supporting the data. The symmetry is restored at large learning times through the diffusion of the receptive field over the invariant manifold; hence, the RBM effectively spans a continuous attractor in the space of network weights. This symmetry-breaking phenomenon takes place only if the amount of data available for training exceeds some critical value, depending on the network size and the intensity of symmetry-induced correlations in the data; below this 'retarded-learning' threshold, the network weights are essentially noisy and overfit the data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge