One-class Recommendation Systems with the Hinge Pairwise Distance Loss and Orthogonal Representations

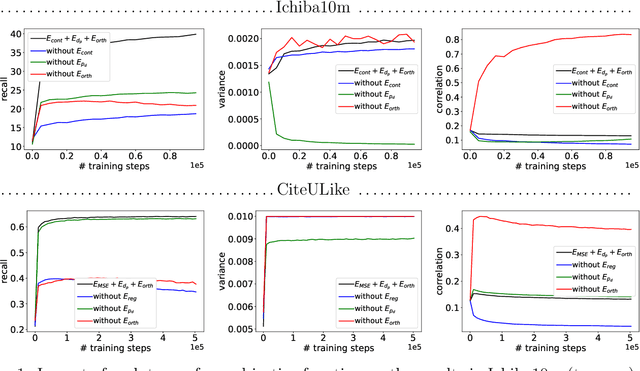
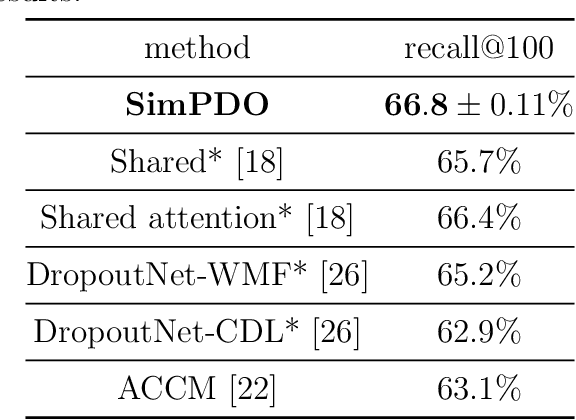
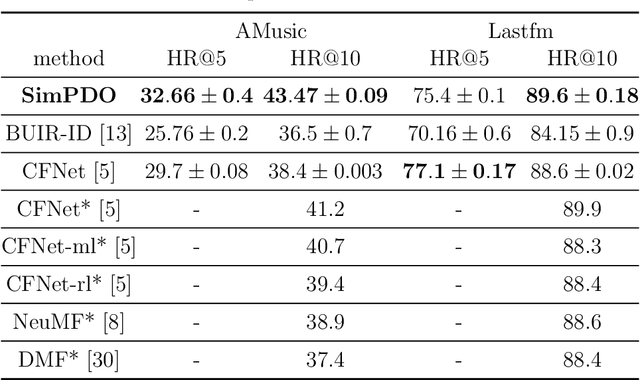
In one-class recommendation systems, the goal is to learn a model from a small set of interacted users and items and then identify the positively-related user-item pairs among a large number of pairs with unknown interactions. Most previous loss functions rely on dissimilar pairs of users and items, which are selected from the ones with unknown interactions, to obtain better prediction performance. This strategy introduces several challenges such as increasing training time and hurting the performance by picking "similar pairs with the unknown interactions" as dissimilar pairs. In this paper, the goal is to only use the similar set to train the models. We point out three trivial solutions that the models converge to when they are trained only on similar pairs: collapsed, partially collapsed, and shrinking solutions. We propose two terms that can be added to the objective functions in the literature to avoid these solutions. The first one is a hinge pairwise distance loss that avoids the shrinking and collapsed solutions by keeping the average pairwise distance of all the representations greater than a margin. The second one is an orthogonality term that minimizes the correlation between the dimensions of the representations and avoids the partially collapsed solution. We conduct experiments on a variety of tasks on public and real-world datasets. The results show that our approach using only similar pairs outperforms state-of-the-art methods using similar pairs and a large number of dissimilar pairs.

Simultaneous Learning of the Inputs and Parameters in Neural Collaborative Filtering

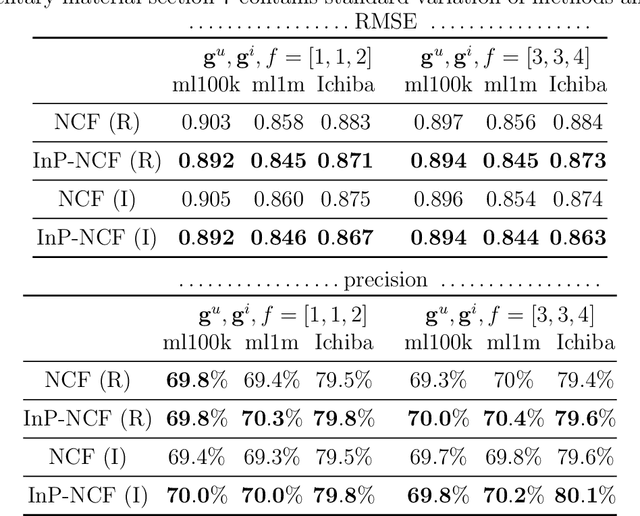
Neural network-based collaborative filtering systems focus on designing network architectures to learn better representations while fixing the input to the user/item interaction vectors and/or ID. In this paper, we first show that the non-zero elements of the inputs are learnable parameters that determine the weights in combining the user/item embeddings, and fixing them limits the power of the models in learning the representations. Then, we propose to learn the value of the non-zero elements of the inputs jointly with the neural network parameters. We analyze the model complexity and the empirical risk of our approach and prove that learning the input leads to a better generalization bound. Our experiments on several real-world datasets show that our method outperforms the state-of-the-art methods, even using shallow network structures with a smaller number of layers and parameters.

Estimating Vector Fields from Noisy Time Series

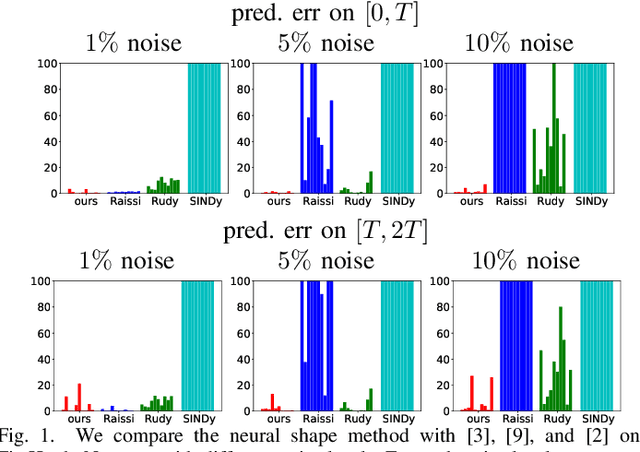
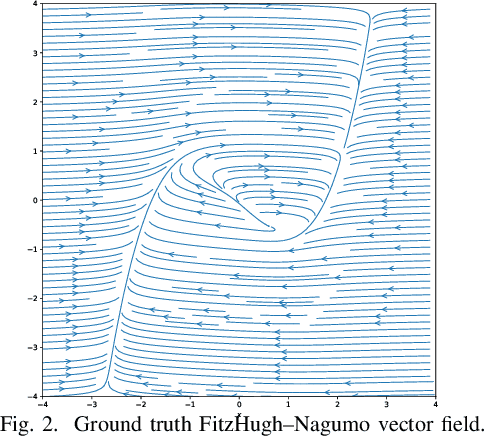
While there has been a surge of recent interest in learning differential equation models from time series, methods in this area typically cannot cope with highly noisy data. We break this problem into two parts: (i) approximating the unknown vector field (or right-hand side) of the differential equation, and (ii) dealing with noise. To deal with (i), we describe a neural network architecture consisting of tensor products of one-dimensional neural shape functions. For (ii), we propose an alternating minimization scheme that switches between vector field training and filtering steps, together with multiple trajectories of training data. We find that the neural shape function architecture retains the approximation properties of dense neural networks, enables effective computation of vector field error, and allows for graphical interpretability, all for data/systems in any finite dimension $d$. We also study the combination of either our neural shape function method or existing differential equation learning methods with alternating minimization and multiple trajectories. We find that retrofitting any learning method in this way boosts the method's robustness to noise. While in their raw form the methods struggle with 1% Gaussian noise, after retrofitting, they learn accurate vector fields from data with 10% Gaussian noise.

Neural Representations in Hybrid Recommender Systems: Prediction versus Regularization

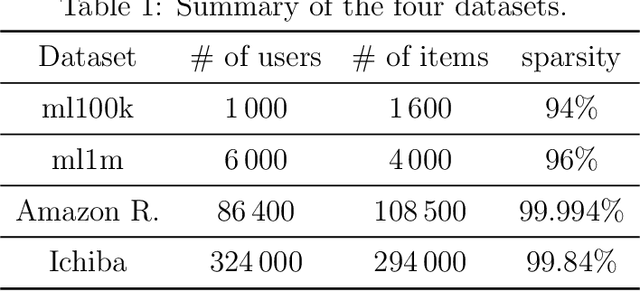
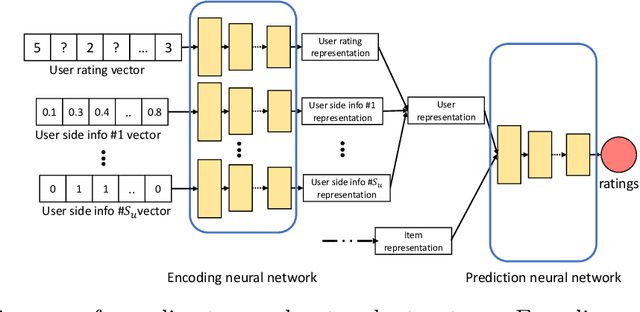
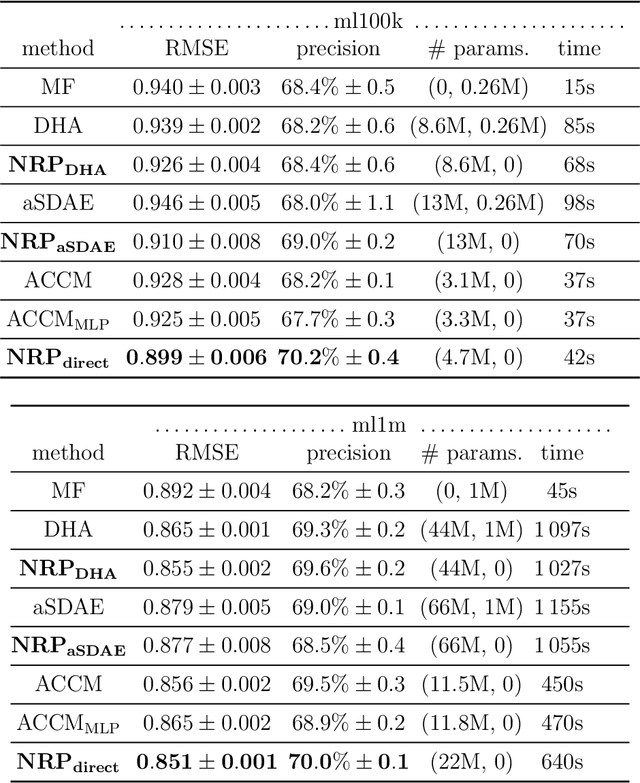
Autoencoder-based hybrid recommender systems have become popular recently because of their ability to learn user and item representations by reconstructing various information sources, including users' feedback on items (e.g., ratings) and side information of users and items (e.g., users' occupation and items' title). However, existing systems still use representations learned by matrix factorization (MF) to predict the rating, while using representations learned by neural networks as the regularizer. In this paper, we define the neural representation for prediction (NRP) framework and apply it to the autoencoder-based recommendation systems. We theoretically analyze how our objective function is related to the previous MF and autoencoder-based methods and explain what it means to use neural representations as the regularizer. We also apply the NRP framework to a direct neural network structure which predicts the ratings without reconstructing the user and item information. We conduct extensive experiments on two MovieLens datasets and two real-world e-commerce datasets. The results confirm that neural representations are better for prediction than regularization and show that the NRP framework, combined with the direct neural network structure, outperforms the state-of-the-art methods in the prediction task, with less training time and memory.

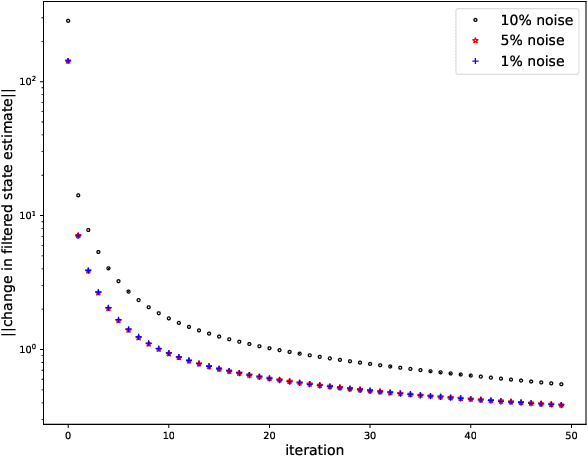
A Direct Method to Learn States and Parameters of Ordinary Differential Equations

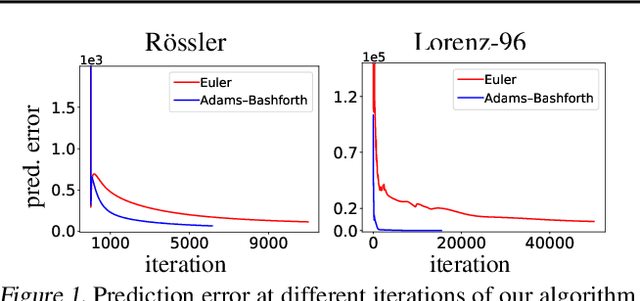
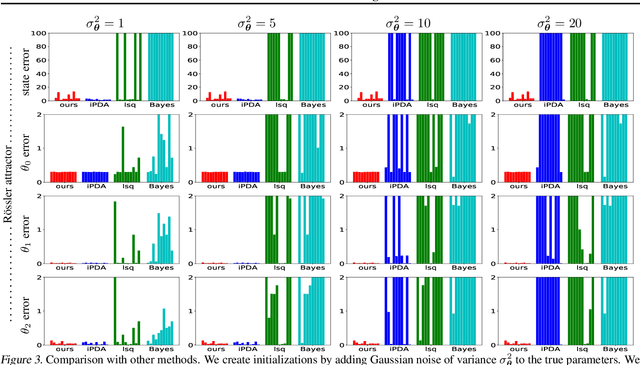
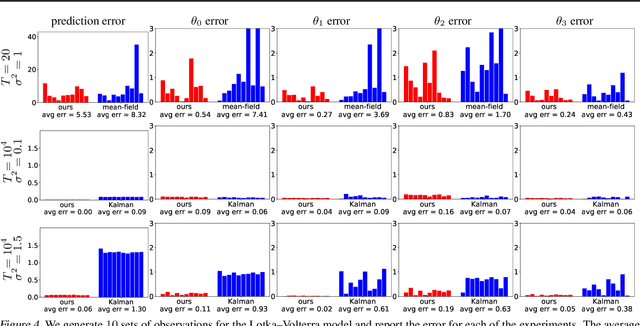
Though ordinary differential equations (ODE) are used extensively in science and engineering, the task of learning ODE parameters from noisy observations still presents challenges. To address these challenges, we propose a direct method that involves alternating minimization of an objective function over the filtered states and parameters. This objective function directly measures how well the filtered states and parameters satisfy the ODE, in contrast to many existing methods that use separate objectives over the observations, filtered states, and parameters. As we show on several ODE systems, as compared to state-of-the-art methods, the direct method exhibits increased robustness (to noise, parameter initialization, and hyperparameters), decreased training times, and improved accuracy in estimating both filtered states and parameters. The direct method involves only one hyperparameter that plays the role of an inverse step size. We show how the direct method can be used with general multistep numerical discretizations, and demonstrate its performance on systems with up to d=40 dimensions. The code of our algorithms can be found in the authors' web pages.

Optimizing affinity-based binary hashing using auxiliary coordinates

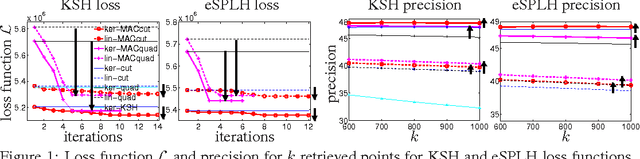
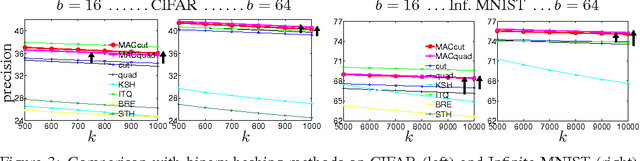
In supervised binary hashing, one wants to learn a function that maps a high-dimensional feature vector to a vector of binary codes, for application to fast image retrieval. This typically results in a difficult optimization problem, nonconvex and nonsmooth, because of the discrete variables involved. Much work has simply relaxed the problem during training, solving a continuous optimization, and truncating the codes a posteriori. This gives reasonable results but is quite suboptimal. Recent work has tried to optimize the objective directly over the binary codes and achieved better results, but the hash function was still learned a posteriori, which remains suboptimal. We propose a general framework for learning hash functions using affinity-based loss functions that uses auxiliary coordinates. This closes the loop and optimizes jointly over the hash functions and the binary codes so that they gradually match each other. The resulting algorithm can be seen as a corrected, iterated version of the procedure of optimizing first over the codes and then learning the hash function. Compared to this, our optimization is guaranteed to obtain better hash functions while being not much slower, as demonstrated experimentally in various supervised datasets. In addition, our framework facilitates the design of optimization algorithms for arbitrary types of loss and hash functions.

An ensemble diversity approach to supervised binary hashing

Binary hashing is a well-known approach for fast approximate nearest-neighbor search in information retrieval. Much work has focused on affinity-based objective functions involving the hash functions or binary codes. These objective functions encode neighborhood information between data points and are often inspired by manifold learning algorithms. They ensure that the hash functions differ from each other through constraints or penalty terms that encourage codes to be orthogonal or dissimilar across bits, but this couples the binary variables and complicates the already difficult optimization. We propose a much simpler approach: we train each hash function (or bit) independently from each other, but introduce diversity among them using techniques from classifier ensembles. Surprisingly, we find that not only is this faster and trivially parallelizable, but it also improves over the more complex, coupled objective function, and achieves state-of-the-art precision and recall in experiments with image retrieval.

Hashing with binary autoencoders

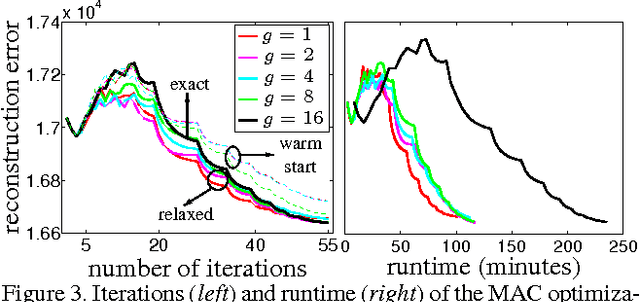
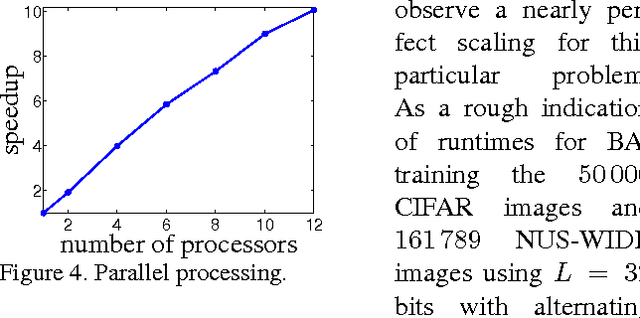
An attractive approach for fast search in image databases is binary hashing, where each high-dimensional, real-valued image is mapped onto a low-dimensional, binary vector and the search is done in this binary space. Finding the optimal hash function is difficult because it involves binary constraints, and most approaches approximate the optimization by relaxing the constraints and then binarizing the result. Here, we focus on the binary autoencoder model, which seeks to reconstruct an image from the binary code produced by the hash function. We show that the optimization can be simplified with the method of auxiliary coordinates. This reformulates the optimization as alternating two easier steps: one that learns the encoder and decoder separately, and one that optimizes the code for each image. Image retrieval experiments, using precision/recall and a measure of code utilization, show the resulting hash function outperforms or is competitive with state-of-the-art methods for binary hashing.