A Direct Method to Learn States and Parameters of Ordinary Differential Equations
Paper and Code
Oct 16, 2018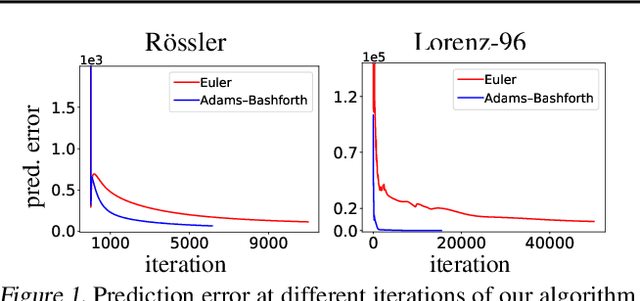

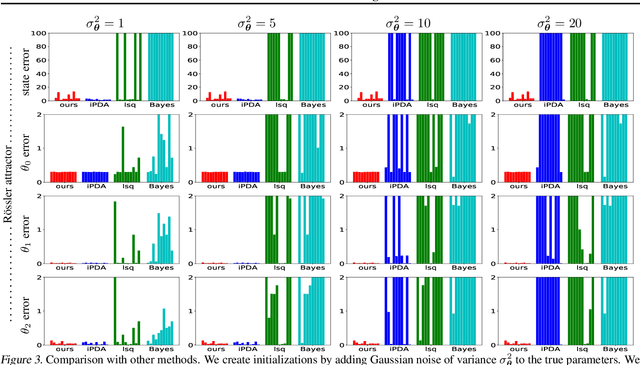
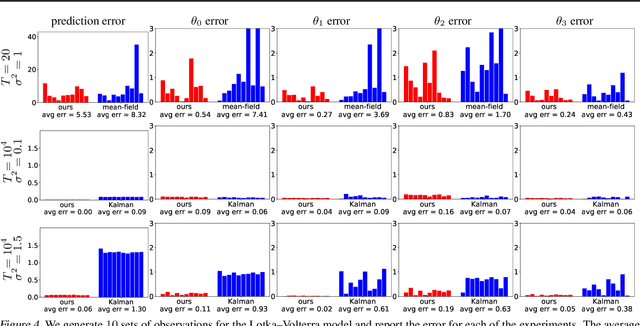
Though ordinary differential equations (ODE) are used extensively in science and engineering, the task of learning ODE parameters from noisy observations still presents challenges. To address these challenges, we propose a direct method that involves alternating minimization of an objective function over the filtered states and parameters. This objective function directly measures how well the filtered states and parameters satisfy the ODE, in contrast to many existing methods that use separate objectives over the observations, filtered states, and parameters. As we show on several ODE systems, as compared to state-of-the-art methods, the direct method exhibits increased robustness (to noise, parameter initialization, and hyperparameters), decreased training times, and improved accuracy in estimating both filtered states and parameters. The direct method involves only one hyperparameter that plays the role of an inverse step size. We show how the direct method can be used with general multistep numerical discretizations, and demonstrate its performance on systems with up to d=40 dimensions. The code of our algorithms can be found in the authors' web pages.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge