Inverse classification with logistic and softmax classifiers: efficient optimization

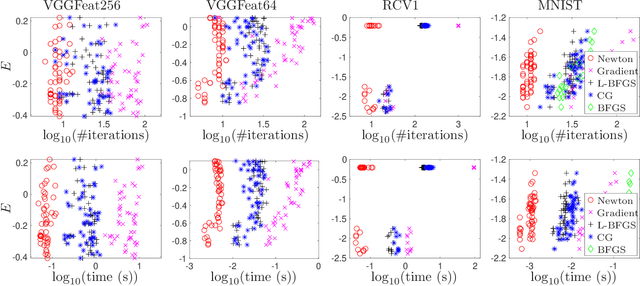
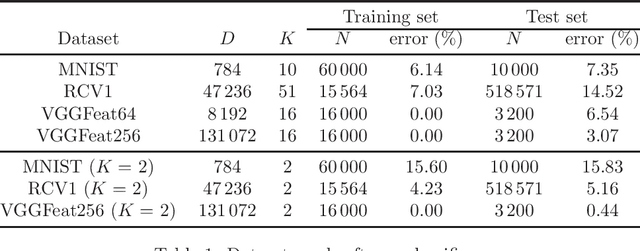
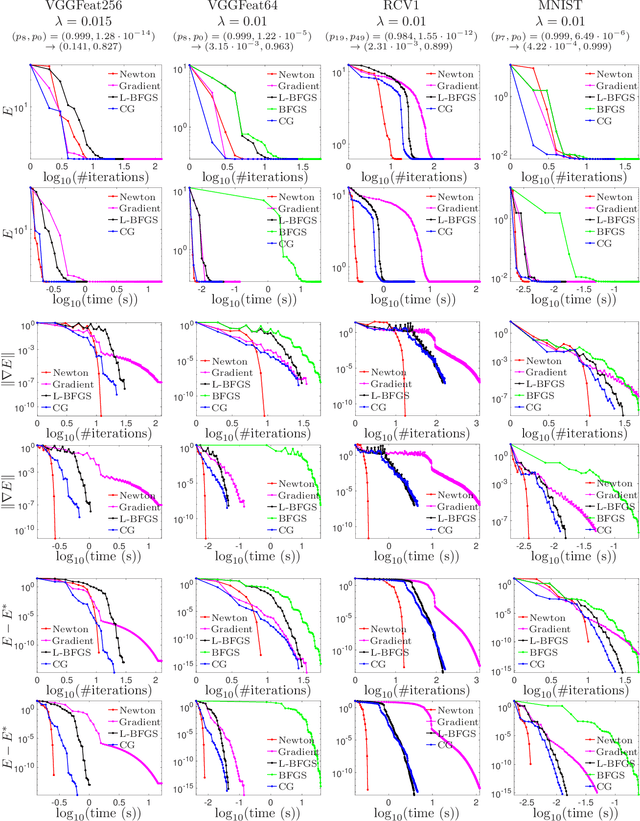
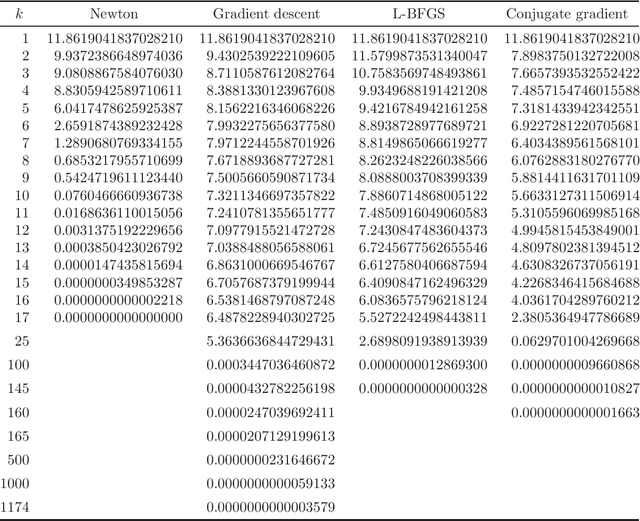
In recent years, a certain type of problems have become of interest where one wants to query a trained classifier. Specifically, one wants to find the closest instance to a given input instance such that the classifier's predicted label is changed in a desired way. Examples of these ``inverse classification'' problems are counterfactual explanations, adversarial examples and model inversion. All of them are fundamentally optimization problems over the input instance vector involving a fixed classifier, and it is of interest to achieve a fast solution for interactive or real-time applications. We focus on solving this problem efficiently for two of the most widely used classifiers: logistic regression and softmax classifiers. Owing to special properties of these models, we show that the optimization can be solved in closed form for logistic regression, and iteratively but extremely fast for the softmax classifier. This allows us to solve either case exactly (to nearly machine precision) in a runtime of milliseconds to around a second even for very high-dimensional instances and many classes.

Solving Recurrence Relations using Machine Learning, with Application to Cost Analysis

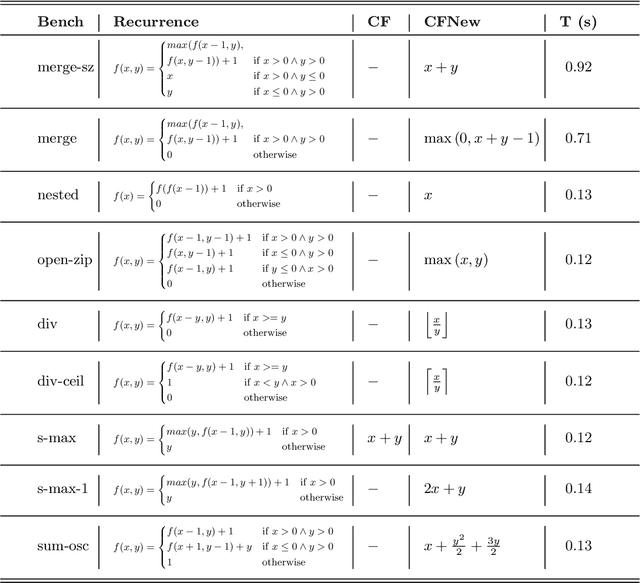
Automatic static cost analysis infers information about the resources used by programs without actually running them with concrete data, and presents such information as functions of input data sizes. Most of the analysis tools for logic programs (and other languages) are based on setting up recurrence relations representing (bounds on) the computational cost of predicates, and solving them to find closed-form functions that are equivalent to (or a bound on) them. Such recurrence solving is a bottleneck in current tools: many of the recurrences that arise during the analysis cannot be solved with current solvers, such as Computer Algebra Systems (CASs), so that specific methods for different classes of recurrences need to be developed. We address such a challenge by developing a novel, general approach for solving arbitrary, constrained recurrence relations, that uses machine-learning sparse regression techniques to guess a candidate closed-form function, and a combination of an SMT-solver and a CAS to check whether such function is actually a solution of the recurrence. We have implemented a prototype and evaluated it with recurrences generated by a cost analysis system (the one in CiaoPP). The experimental results are quite promising, showing that our approach can find closed-form solutions, in a reasonable time, for classes of recurrences that cannot be solved by such a system, nor by current CASs.

Very fast, approximate counterfactual explanations for decision forests

We consider finding a counterfactual explanation for a classification or regression forest, such as a random forest. This requires solving an optimization problem to find the closest input instance to a given instance for which the forest outputs a desired value. Finding an exact solution has a cost that is exponential on the number of leaves in the forest. We propose a simple but very effective approach: we constrain the optimization to only those input space regions defined by the forest that are populated by actual data points. The problem reduces to a form of nearest-neighbor search using a certain distance on a certain dataset. This has two advantages: first, the solution can be found very quickly, scaling to large forests and high-dimensional data, and enabling interactive use. Second, the solution found is more likely to be realistic in that it is guided towards high-density areas of input space.

Model compression as constrained optimization, with application to neural nets. Part V: combining compressions

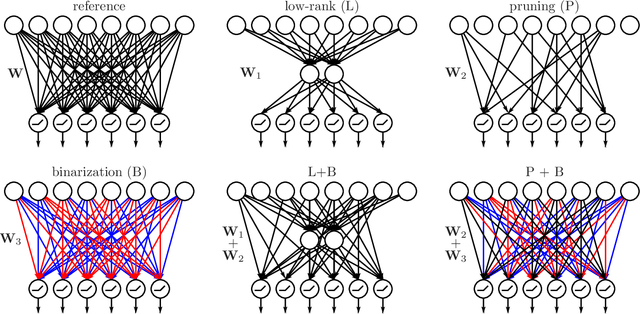
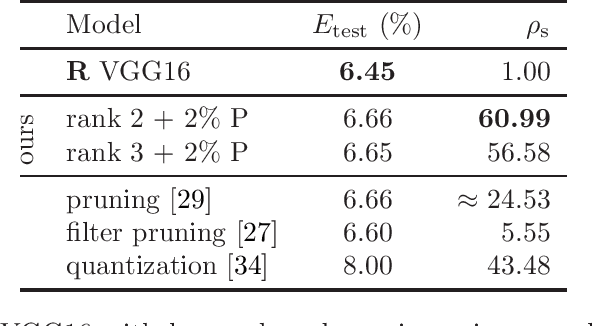
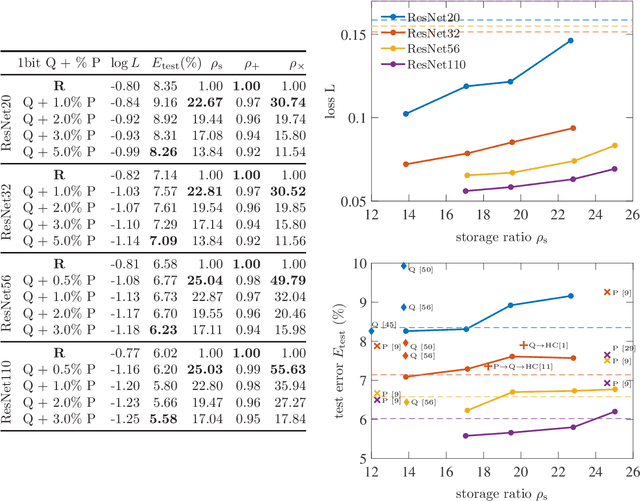
Model compression is generally performed by using quantization, low-rank approximation or pruning, for which various algorithms have been researched in recent years. One fundamental question is: what types of compression work better for a given model? Or even better: can we improve by combining compressions in a suitable way? We formulate this generally as a problem of optimizing the loss but where the weights are constrained to equal an additive combination of separately compressed parts; and we give an algorithm to learn the corresponding parts' parameters. Experimentally with deep neural nets, we observe that 1) we can find significantly better models in the error-compression space, indicating that different compression types have complementary benefits, and 2) the best type of combination depends exquisitely on the type of neural net. For example, we can compress ResNets and AlexNet using only 1 bit per weight without error degradation at the cost of adding a few floating point weights. However, VGG nets can be better compressed by combining low-rank with a few floating point weights.

Sparse Oblique Decision Trees: A Tool to Understand and Manipulate Neural Net Features

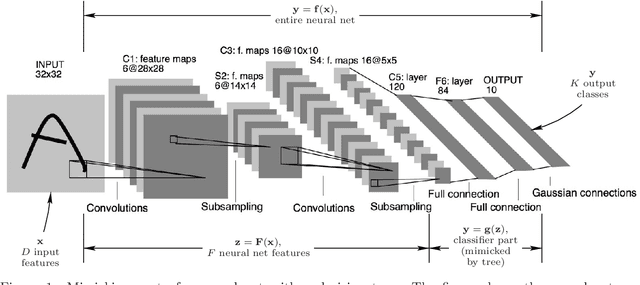
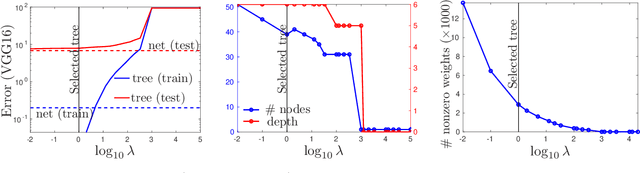
The widespread deployment of deep nets in practical applications has lead to a growing desire to understand how and why such black-box methods perform prediction. Much work has focused on understanding what part of the input pattern (an image, say) is responsible for a particular class being predicted, and how the input may be manipulated to predict a different class. We focus instead on understanding which of the internal features computed by the neural net are responsible for a particular class. We achieve this by mimicking part of the neural net with an oblique decision tree having sparse weight vectors at the decision nodes. Using the recently proposed Tree Alternating Optimization (TAO) algorithm, we are able to learn trees that are both highly accurate and interpretable. Such trees can faithfully mimic the part of the neural net they replaced, and hence they can provide insights into the deep net black box. Further, we show we can easily manipulate the neural net features in order to make the net predict, or not predict, a given class, thus showing that it is possible to carry out adversarial attacks at the level of the features. These insights and manipulations apply globally to the entire training and test set, not just at a local (single-instance) level. We demonstrate this robustly in the MNIST and ImageNet datasets with LeNet5 and VGG networks.

Counterfactual Explanations for Oblique Decision Trees: Exact, Efficient Algorithms

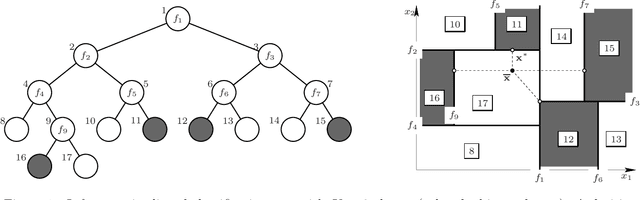
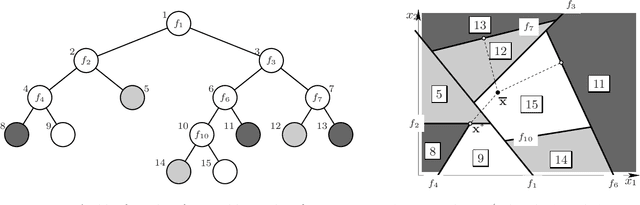
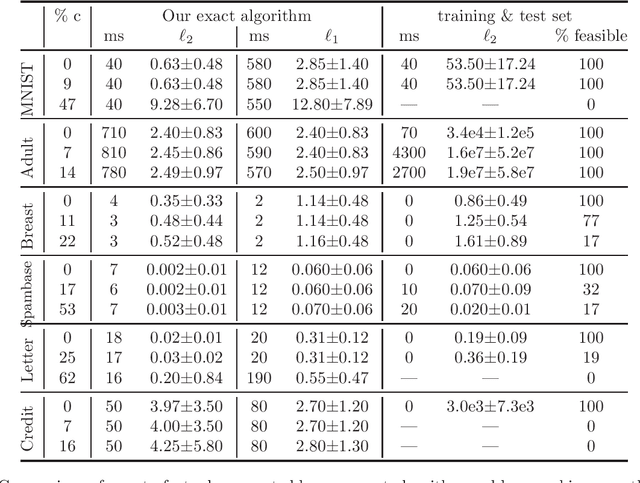
We consider counterfactual explanations, the problem of minimally adjusting features in a source input instance so that it is classified as a target class under a given classifier. This has become a topic of recent interest as a way to query a trained model and suggest possible actions to overturn its decision. Mathematically, the problem is formally equivalent to that of finding adversarial examples, which also has attracted significant attention recently. Most work on either counterfactual explanations or adversarial examples has focused on differentiable classifiers, such as neural nets. We focus on classification trees, both axis-aligned and oblique (having hyperplane splits). Although here the counterfactual optimization problem is nonconvex and nondifferentiable, we show that an exact solution can be computed very efficiently, even with high-dimensional feature vectors and with both continuous and categorical features, and demonstrate it in different datasets and settings. The results are particularly relevant for finance, medicine or legal applications, where interpretability and counterfactual explanations are particularly important.

A flexible, extensible software framework for model compression based on the LC algorithm

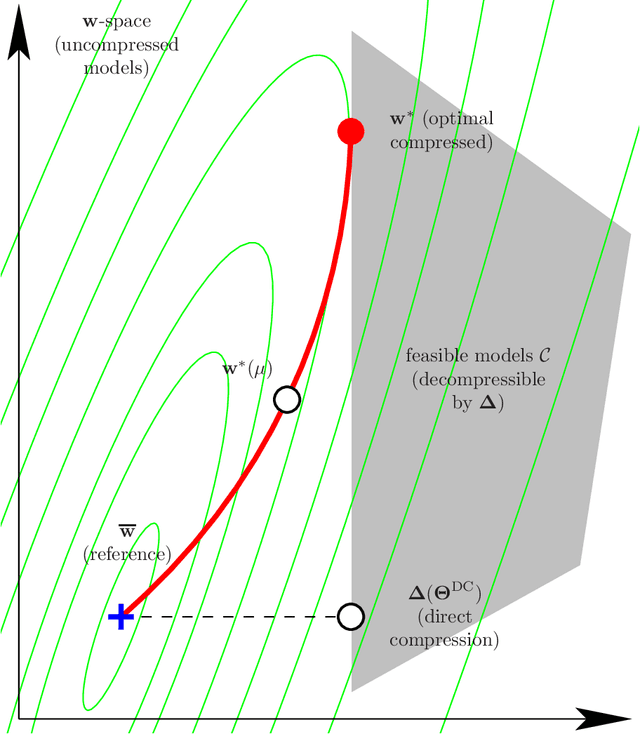
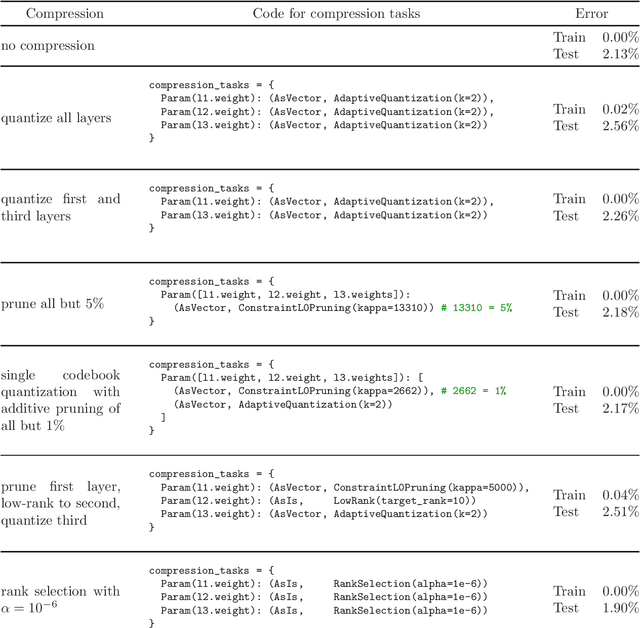
We propose a software framework based on the ideas of the Learning-Compression (LC) algorithm, that allows a user to compress a neural network or other machine learning model using different compression schemes with minimal effort. Currently, the supported compressions include pruning, quantization, low-rank methods (including automatically learning the layer ranks), and combinations of those, and the user can choose different compression types for different parts of a neural network. The LC algorithm alternates two types of steps until convergence: a learning (L) step, which trains a model on a dataset (using an algorithm such as SGD); and a compression (C) step, which compresses the model parameters (using a compression scheme such as low-rank or quantization). This decoupling of the "machine learning" aspect from the "signal compression" aspect means that changing the model or the compression type amounts to calling the corresponding subroutine in the L or C step, respectively. The library fully supports this by design, which makes it flexible and extensible. This does not come at the expense of performance: the runtime needed to compress a model is comparable to that of training the model in the first place; and the compressed model is competitive in terms of prediction accuracy and compression ratio with other algorithms (which are often specialized for specific models or compression schemes). The library is written in Python and PyTorch and available in Github.

An Experimental Comparison of Old and New Decision Tree Algorithms

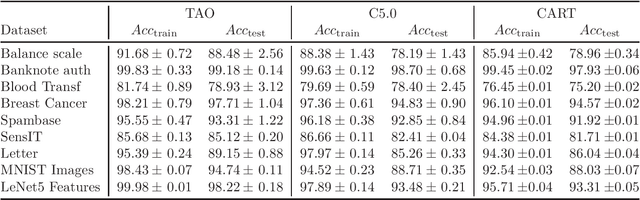
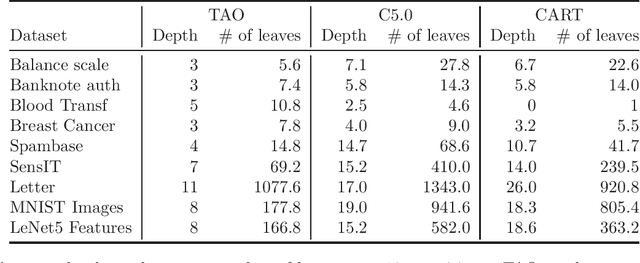
This paper presents a detailed comparison of a recently proposed algorithm for optimizing decision trees, tree alternating optimization (TAO), with other popular, established algorithms, such as CART and C5.0. We compare their performance on a number of datasets of different size, dimensionality and number of classes, across different performance factors: accuracy and tree size (in terms of the number of leaves or the depth of the tree). We find that TAO achieves higher accuracy in every single dataset, often by a large margin.

Style Transfer by Rigid Alignment in Neural Net Feature Space

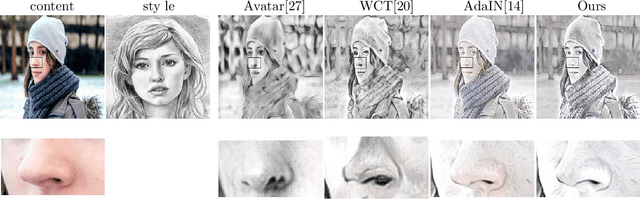
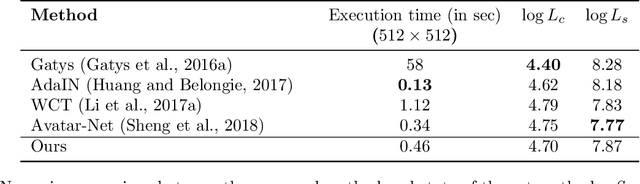
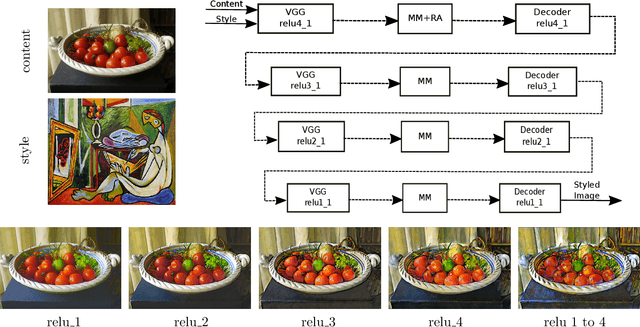
Arbitrary style transfer is an important problem in computer vision that aims to transfer style patterns from an arbitrary style image to a given content image. However, current methods either rely on slow iterative optimization or fast pre-determined feature transformation, but at the cost of compromised visual quality of the styled image; especially, distorted content structure. In this work, we present an effective and efficient approach for arbitrary style transfer that seamlessly transfers style patterns as well as keep content structure intact in the styled image. We achieve this by aligning style features to content features using rigid alignment; thus modifying style features, unlike the existing methods that do the opposite. We demonstrate the effectiveness of the proposed approach by generating high-quality stylized images and compare the results with the current state-of-the-art techniques for arbitrary style transfer.

Sampling the "Inverse Set" of a Neuron: An Approach to Understanding Neural Nets

With the recent success of deep neural networks in computer vision, it is important to understand the internal working of these networks. What does a given neuron represent? The concepts captured by a neuron may be hard to understand or express in simple terms. The approach we propose in this paper is to characterize the region of input space that excites a given neuron to a certain level; we call this the inverse set. This inverse set is a complicated high dimensional object that we explore by an optimization-based sampling approach. Inspection of samples of this set by a human can reveal regularities that help to understand the neuron. This goes beyond approaches which were limited to finding an image which maximally activates the neuron or using Markov chain Monte Carlo to sample images, but this is very slow, generates samples with little diversity and lacks control over the activation value of the generated samples. Our approach also allows us to explore the intersection of inverse sets of several neurons and other variations.