Solving Recurrence Relations using Machine Learning, with Application to Cost Analysis

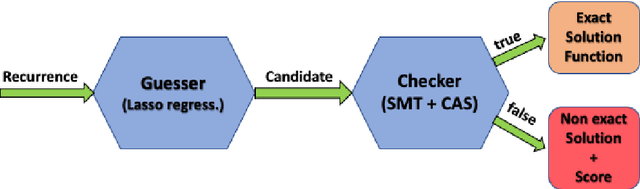
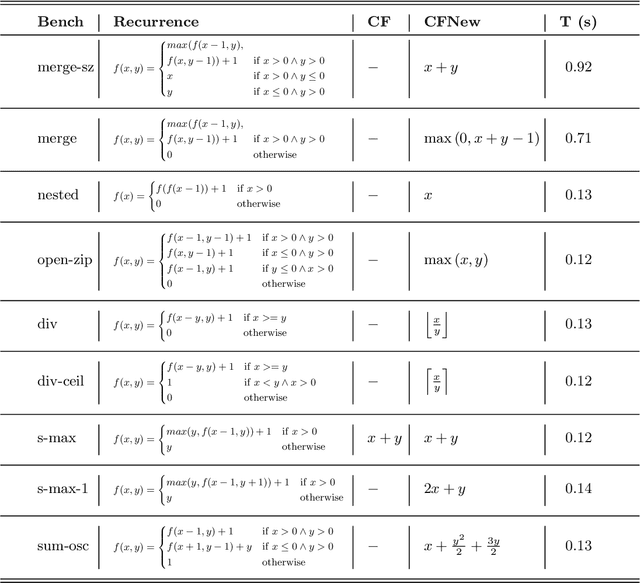
Automatic static cost analysis infers information about the resources used by programs without actually running them with concrete data, and presents such information as functions of input data sizes. Most of the analysis tools for logic programs (and other languages) are based on setting up recurrence relations representing (bounds on) the computational cost of predicates, and solving them to find closed-form functions that are equivalent to (or a bound on) them. Such recurrence solving is a bottleneck in current tools: many of the recurrences that arise during the analysis cannot be solved with current solvers, such as Computer Algebra Systems (CASs), so that specific methods for different classes of recurrences need to be developed. We address such a challenge by developing a novel, general approach for solving arbitrary, constrained recurrence relations, that uses machine-learning sparse regression techniques to guess a candidate closed-form function, and a combination of an SMT-solver and a CAS to check whether such function is actually a solution of the recurrence. We have implemented a prototype and evaluated it with recurrences generated by a cost analysis system (the one in CiaoPP). The experimental results are quite promising, showing that our approach can find closed-form solutions, in a reasonable time, for classes of recurrences that cannot be solved by such a system, nor by current CASs.

An Improved Discrete Bat Algorithm for Symmetric and Asymmetric Traveling Salesman Problems

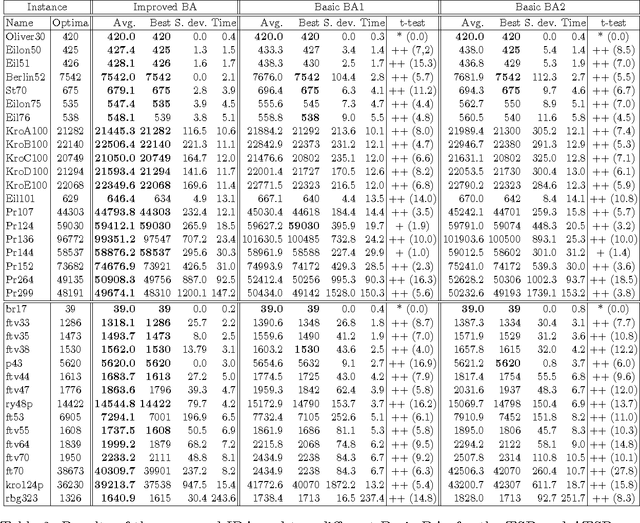
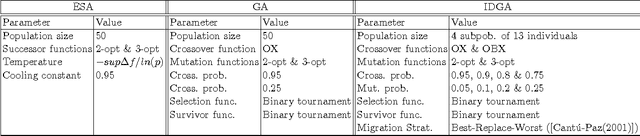
Bat algorithm is a population metaheuristic proposed in 2010 which is based on the echolocation or bio-sonar characteristics of microbats. Since its first implementation, the bat algorithm has been used in a wide range of fields. In this paper, we present a discrete version of the bat algorithm to solve the well-known symmetric and asymmetric traveling salesman problems. In addition, we propose an improvement in the basic structure of the classic bat algorithm. To prove that our proposal is a promising approximation method, we have compared its performance in 37 instances with the results obtained by five different techniques: evolutionary simulated annealing, genetic algorithm, an island based distributed genetic algorithm, a discrete firefly algorithm and an imperialist competitive algorithm. In order to obtain fair and rigorous comparisons, we have conducted three different statistical tests along the paper: the Student's $t$-test, the Holm's test, and the Friedman test. We have also compared the convergence behaviour shown by our proposal with the ones shown by the evolutionary simulated annealing, and the discrete firefly algorithm. The experimentation carried out in this study has shown that the presented improved bat algorithm outperforms significantly all the other alternatives in most of the cases.