Linear Inverse Problems Using a Generative Compound Gaussian Prior

Since most inverse problems arising in scientific and engineering applications are ill-posed, prior information about the solution space is incorporated, typically through regularization, to establish a well-posed problem with a unique solution. Often, this prior information is an assumed statistical distribution of the desired inverse problem solution. Recently, due to the unprecedented success of generative adversarial networks (GANs), the generative network from a GAN has been implemented as the prior information in imaging inverse problems. In this paper, we devise a novel iterative algorithm to solve inverse problems in imaging where a dual-structured prior is imposed by combining a GAN prior with the compound Gaussian (CG) class of distributions. A rigorous computational theory for the convergence of the proposed iterative algorithm, which is based upon the alternating direction method of multipliers, is established. Furthermore, elaborate empirical results for the proposed iterative algorithm are presented. By jointly exploiting the powerful CG and GAN classes of image priors, we find, in compressive sensing and tomographic imaging problems, our proposed algorithm outperforms and provides improved generalizability over competitive prior art approaches while avoiding performance saturation issues in previous GAN prior-based methods.

Robust and tractable multidimensional exponential analysis

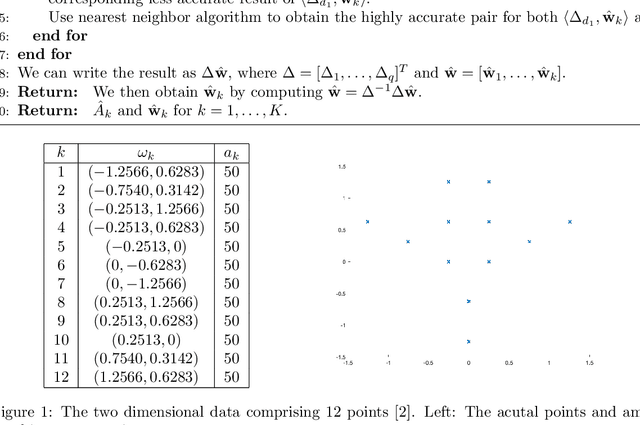
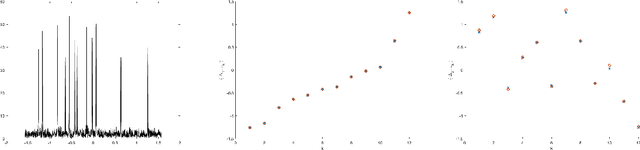
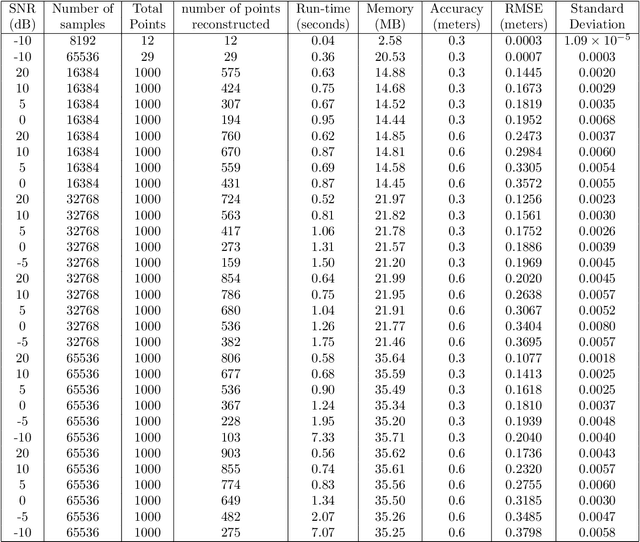
Motivated by a number of applications in signal processing, we study the following question. Given samples of a multidimensional signal of the form \begin{align*} f(\bs\ell)=\sum_{k=1}^K a_k\exp(-i\langle \bs\ell, \w_k\rangle), \\ \w_1,\cdots,\w_k\in\mathbb{R}^q, \ \bs\ell\in \ZZ^q, \ |\bs\ell| <n, \end{align*} determine the values of the number $K$ of components, and the parameters $a_k$ and $\w_k$'s. We develop an algorithm to recuperate these quantities accurately using only a subsample of size $\O(qn)$ of this data. For this purpose, we use a novel localized kernel method to identify the parameters, including the number $K$ of signals. Our method is easy to implement, and is shown to be stable under a very low SNR range. We demonstrate the effectiveness of our resulting algorithm using 2 and 3 dimensional examples from the literature, and show substantial improvements over state-of-the-art techniques including Prony based, MUSIC and ESPRIT approaches.

On Generalization Bounds for Deep Compound Gaussian Neural Networks

Algorithm unfolding or unrolling is the technique of constructing a deep neural network (DNN) from an iterative algorithm. Unrolled DNNs often provide better interpretability and superior empirical performance over standard DNNs in signal estimation tasks. An important theoretical question, which has only recently received attention, is the development of generalization error bounds for unrolled DNNs. These bounds deliver theoretical and practical insights into the performance of a DNN on empirical datasets that are distinct from, but sampled from, the probability density generating the DNN training data. In this paper, we develop novel generalization error bounds for a class of unrolled DNNs that are informed by a compound Gaussian prior. These compound Gaussian networks have been shown to outperform comparative standard and unfolded deep neural networks in compressive sensing and tomographic imaging problems. The generalization error bound is formulated by bounding the Rademacher complexity of the class of compound Gaussian network estimates with Dudley's integral. Under realistic conditions, we show that, at worst, the generalization error scales $\mathcal{O}(n\sqrt{\ln(n)})$ in the signal dimension and $\mathcal{O}(($Network Size$)^{3/2})$ in network size.

Deep Regularized Compound Gaussian Network for Solving Linear Inverse Problems

Incorporating prior information into inverse problems, e.g. via maximum-a-posteriori estimation, is an important technique for facilitating robust inverse problem solutions. In this paper, we devise two novel approaches for linear inverse problems that permit problem-specific statistical prior selections within the compound Gaussian (CG) class of distributions. The CG class subsumes many commonly used priors in signal and image reconstruction methods including those of sparsity-based approaches. The first method developed is an iterative algorithm, called generalized compound Gaussian least squares (G-CG-LS), that minimizes a regularized least squares objective function where the regularization enforces a CG prior. G-CG-LS is then unrolled, or unfolded, to furnish our second method, which is a novel deep regularized (DR) neural network, called DR-CG-Net, that learns the prior information. A detailed computational theory on convergence properties of G-CG-LS and thorough numerical experiments for DR-CG-Net are provided. Due to the comprehensive nature of the CG prior, these experiments show that our unrolled DR-CG-Net outperforms competitive prior art methods in tomographic imaging and compressive sensing, especially in challenging low-training scenarios.

A Compound Gaussian Network for Solving Linear Inverse Problems

For solving linear inverse problems, particularly of the type that appear in tomographic imaging and compressive sensing, this paper develops two new approaches. The first approach is an iterative algorithm that minimizers a regularized least squares objective function where the regularization is based on a compound Gaussian prior distribution. The Compound Gaussian prior subsumes many of the commonly used priors in image reconstruction, including those of sparsity-based approaches. The developed iterative algorithm gives rise to the paper's second new approach, which is a deep neural network that corresponds to an "unrolling" or "unfolding" of the iterative algorithm. Unrolled deep neural networks have interpretable layers and outperform standard deep learning methods. This paper includes a detailed computational theory that provides insight into the construction and performance of both algorithms. The conclusion is that both algorithms outperform other state-of-the-art approaches to tomographic image formation and compressive sensing, especially in the difficult regime of low training.

Nonparametric Decentralized Detection and Sparse Sensor Selection via Multi-Sensor Online Kernel Scalar Quantization

Signal classification problems arise in a wide variety of applications, and their demand is only expected to grow. In this paper, we focus on the wireless sensor network signal classification setting, where each sensor forwards quantized signals to a fusion center to be classified. Our primary goal is to train a decision function and quantizers across the sensors to maximize the classification performance in an online manner. Moreover, we are interested in sparse sensor selection using a marginalized weighted kernel approach to improve network resource efficiency by disabling less reliable sensors with minimal effect on classification performance.To achieve our goals, we develop a multi-sensor online kernel scalar quantization (MSOKSQ) learning strategy that operates on the sensor outputs at the fusion center. Our theoretical analysis reveals how the proposed algorithm affects the quantizers across the sensors. Additionally, we provide a convergence analysis of our online learning approach by studying its relationship to batch learning. We conduct numerical studies under different classification and sensor network settings which demonstrate the accuracy gains from optimizing different components of MSOKSQ and robustness to reduction in the number of sensors selected.

An Online Stochastic Kernel Machine for Robust Signal Classification

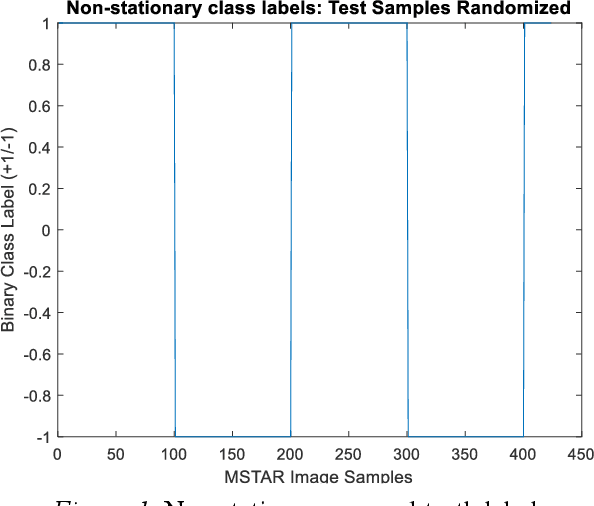
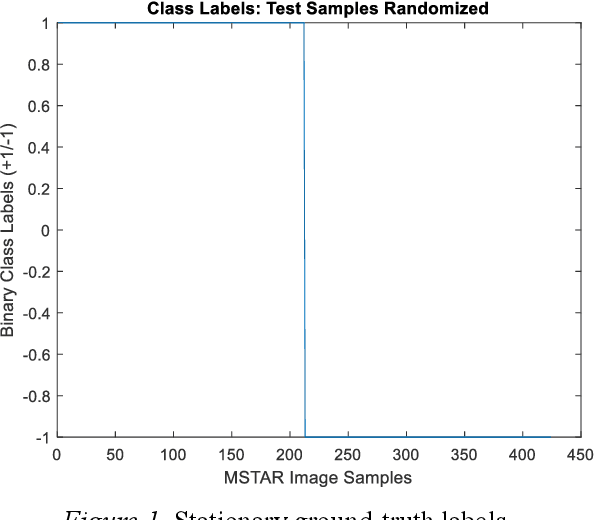
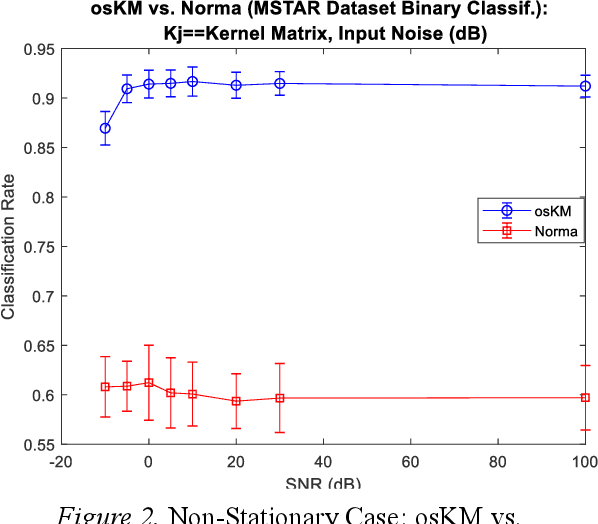
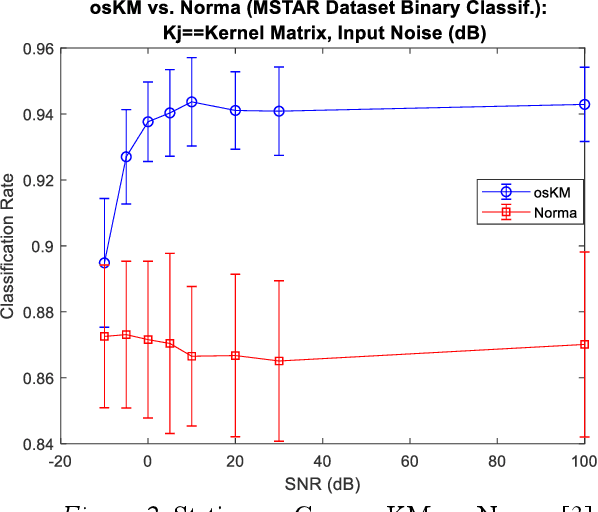
We present a novel variation of online kernel machines in which we exploit a consensus based optimization mechanism to guide the evolution of decision functions drawn from a reproducing kernel Hilbert space, which efficiently models the observed stationary process.

Fast Stochastic Hierarchical Bayesian MAP for Tomographic Imaging

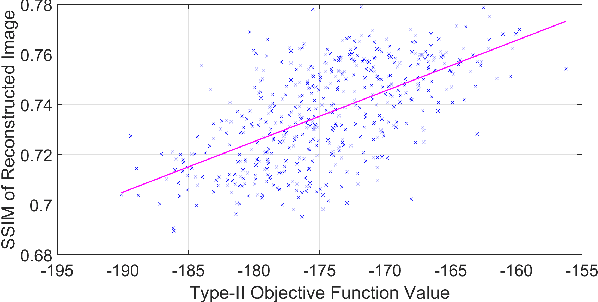
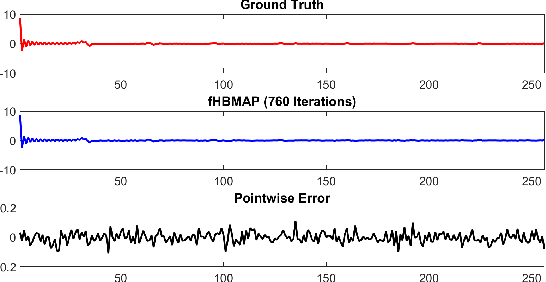
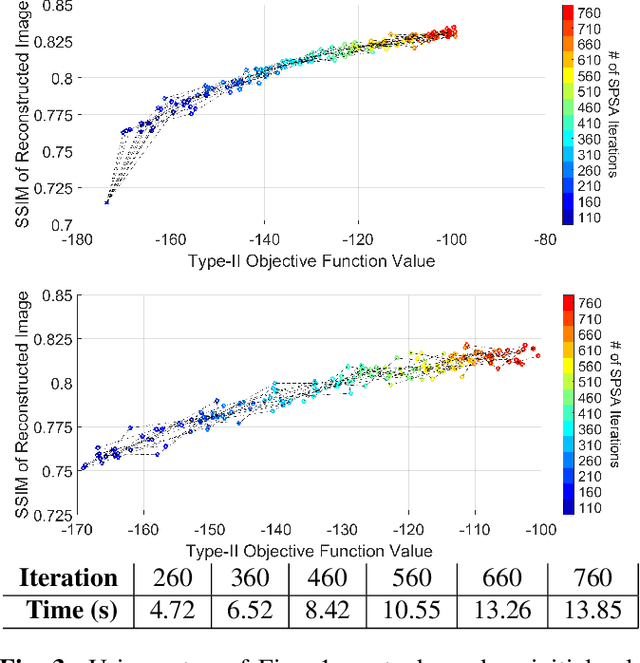
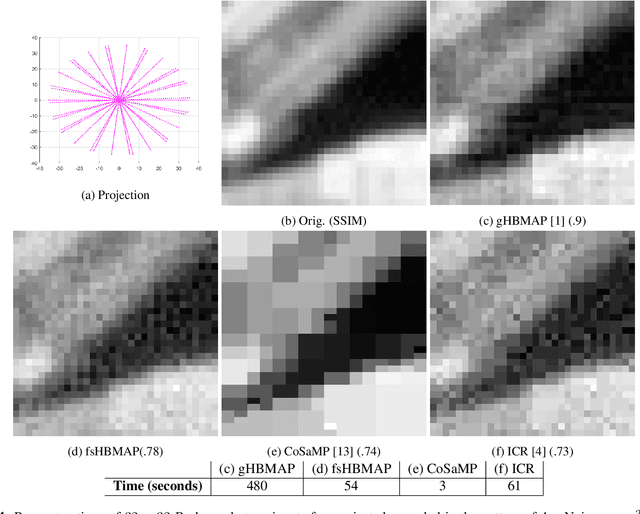
Any image recovery algorithm attempts to achieve the highest quality reconstruction in a timely manner. The former can be achieved in several ways, among which are by incorporating Bayesian priors that exploit natural image tendencies to cue in on relevant phenomena. The Hierarchical Bayesian MAP (HB-MAP) is one such approach which is known to produce compelling results albeit at a substantial computational cost. We look to provide further analysis and insights into what makes the HB-MAP work. While retaining the proficient nature of HB-MAP's Type-I estimation, we propose a stochastic approximation-based approach to Type-II estimation. The resulting algorithm, fast stochastic HB-MAP (fsHBMAP), takes dramatically fewer operations while retaining high reconstruction quality. We employ our fsHBMAP scheme towards the problem of tomographic imaging and demonstrate that fsHBMAP furnishes promising results when compared to many competing methods.

Robust Sonar ATR Through Bayesian Pose Corrected Sparse Classification

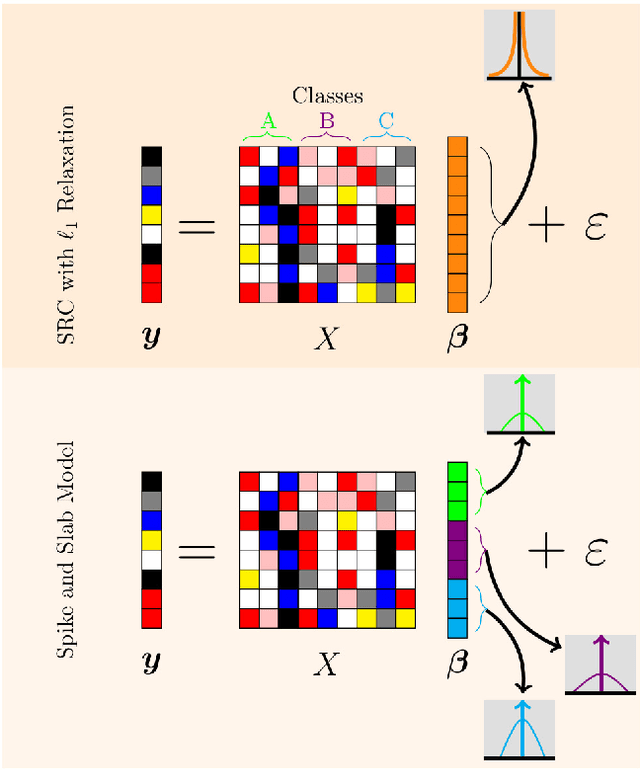
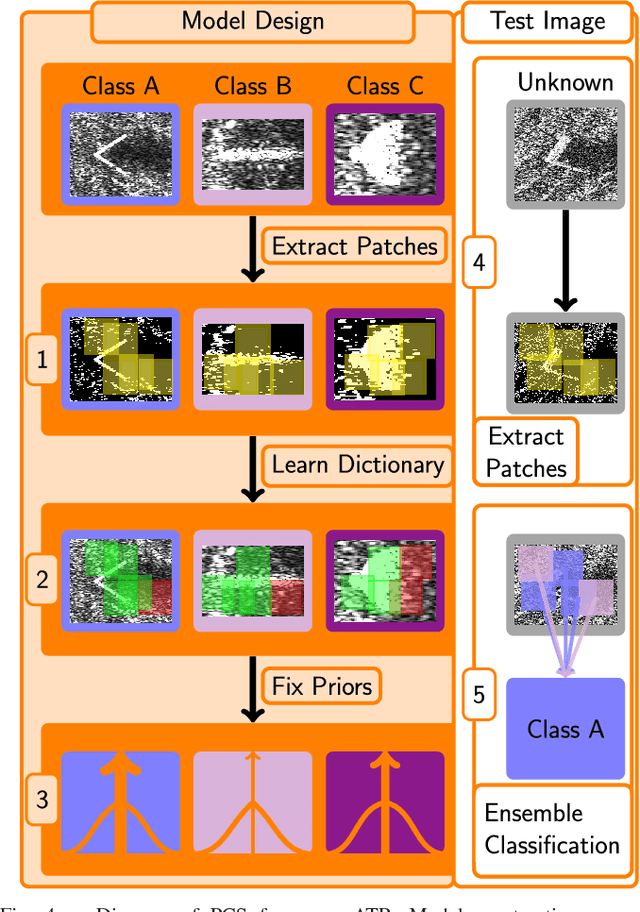
Sonar imaging has seen vast improvements over the last few decades due in part to advances in synthetic aperture Sonar (SAS). Sophisticated classification techniques can now be used in Sonar automatic target recognition (ATR) to locate mines and other threatening objects. Among the most promising of these methods is sparse reconstruction-based classification (SRC) which has shown an impressive resiliency to noise, blur, and occlusion. We present a coherent strategy for expanding upon SRC for Sonar ATR that retains SRC's robustness while also being able to handle targets with diverse geometric arrangements, bothersome Rayleigh noise, and unavoidable background clutter. Our method, pose corrected sparsity (PCS), incorporates a novel interpretation of a spike and slab probability distribution towards use as a Bayesian prior for class-specific discrimination in combination with a dictionary learning scheme for localized patch extractions. Additionally, PCS offers the potential for anomaly detection in order to avoid false identifications of tested objects from outside the training set with no additional training required. Compelling results are shown using a database provided by the United States Naval Surface Warfare Center.