Robust and tractable multidimensional exponential analysis

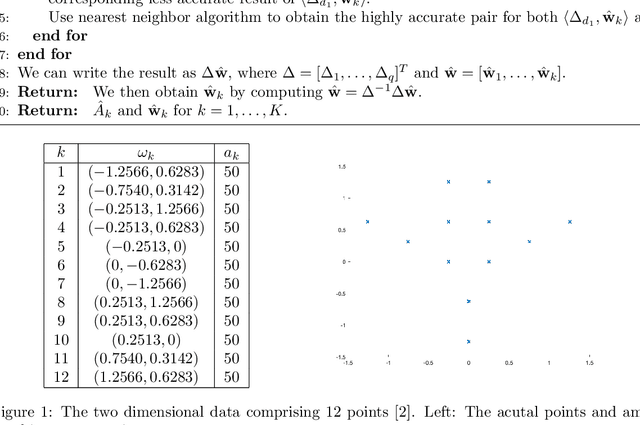
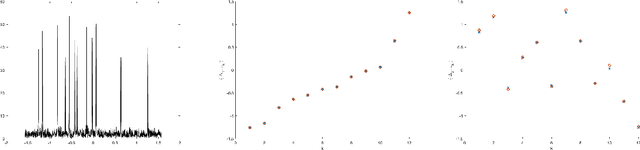
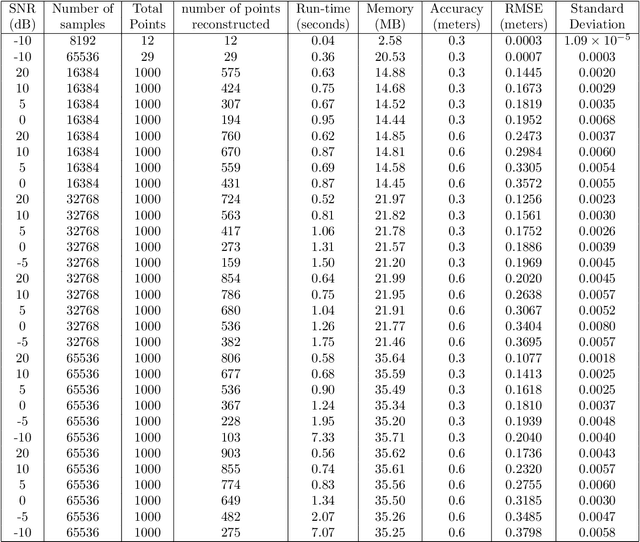
Motivated by a number of applications in signal processing, we study the following question. Given samples of a multidimensional signal of the form \begin{align*} f(\bs\ell)=\sum_{k=1}^K a_k\exp(-i\langle \bs\ell, \w_k\rangle), \\ \w_1,\cdots,\w_k\in\mathbb{R}^q, \ \bs\ell\in \ZZ^q, \ |\bs\ell| <n, \end{align*} determine the values of the number $K$ of components, and the parameters $a_k$ and $\w_k$'s. We develop an algorithm to recuperate these quantities accurately using only a subsample of size $\O(qn)$ of this data. For this purpose, we use a novel localized kernel method to identify the parameters, including the number $K$ of signals. Our method is easy to implement, and is shown to be stable under a very low SNR range. We demonstrate the effectiveness of our resulting algorithm using 2 and 3 dimensional examples from the literature, and show substantial improvements over state-of-the-art techniques including Prony based, MUSIC and ESPRIT approaches.

Learning on manifolds without manifold learning

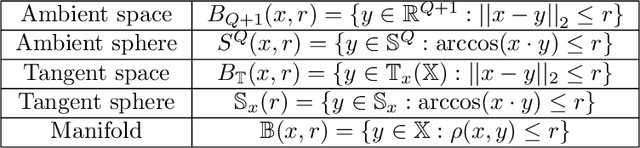
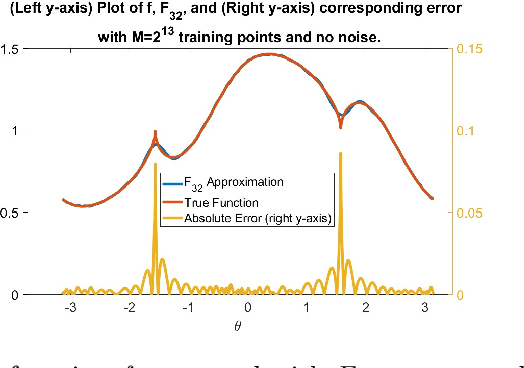
Function approximation based on data drawn randomly from an unknown distribution is an important problem in machine learning. In contrast to the prevalent paradigm of solving this problem by minimizing a loss functional, we have given a direct one-shot construction together with optimal error bounds under the manifold assumption; i.e., one assumes that the data is sampled from an unknown sub-manifold of a high dimensional Euclidean space. A great deal of research deals with obtaining information about this manifold, such as the eigendecomposition of the Laplace-Beltrami operator or coordinate charts, and using this information for function approximation. This two step approach implies some extra errors in the approximation stemming from basic quantities of the data in addition to the errors inherent in function approximation. In Neural Networks, 132:253268, 2020, we have proposed a one-shot direct method to achieve function approximation without requiring the extraction of any information about the manifold other than its dimension. However, one cannot pin down the class of approximants used in that paper. In this paper, we view the unknown manifold as a sub-manifold of an ambient hypersphere and study the question of constructing a one-shot approximation using the spherical polynomials based on the hypersphere. Our approach does not require preprocessing of the data to obtain information about the manifold other than its dimension. We give optimal rates of approximation for relatively "rough" functions.

Local transfer learning from one data space to another

A fundamental problem in manifold learning is to approximate a functional relationship in a data chosen randomly from a probability distribution supported on a low dimensional sub-manifold of a high dimensional ambient Euclidean space. The manifold is essentially defined by the data set itself and, typically, designed so that the data is dense on the manifold in some sense. The notion of a data space is an abstraction of a manifold encapsulating the essential properties that allow for function approximation. The problem of transfer learning (meta-learning) is to use the learning of a function on one data set to learn a similar function on a new data set. In terms of function approximation, this means lifting a function on one data space (the base data space) to another (the target data space). This viewpoint enables us to connect some inverse problems in applied mathematics (such as inverse Radon transform) with transfer learning. In this paper we examine the question of such lifting when the data is assumed to be known only on a part of the base data space. We are interested in determining subsets of the target data space on which the lifting can be defined, and how the local smoothness of the function and its lifting are related.

A function approximation approach to the prediction of blood glucose levels

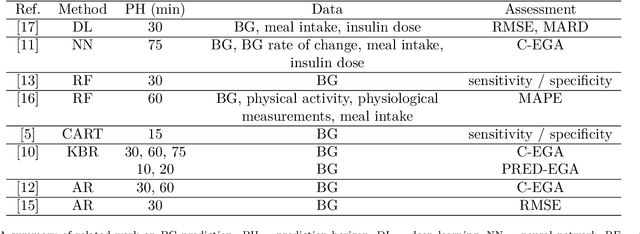
The problem of real time prediction of blood glucose (BG) levels based on the readings from a continuous glucose monitoring (CGM) device is a problem of great importance in diabetes care, and therefore, has attracted a lot of research in recent years, especially based on machine learning. An accurate prediction with a 30, 60, or 90 minute prediction horizon has the potential of saving millions of dollars in emergency care costs. In this paper, we treat the problem as one of function approximation, where the value of the BG level at time $t+h$ (where $h$ the prediction horizon) is considered to be an unknown function of $d$ readings prior to the time $t$. This unknown function may be supported in particular on some unknown submanifold of the $d$-dimensional Euclidean space. While manifold learning is classically done in a semi-supervised setting, where the entire data has to be known in advance, we use recent ideas to achieve an accurate function approximation in a supervised setting; i.e., construct a model for the target function. We use the state-of-the-art clinically relevant PRED-EGA grid to evaluate our results, and demonstrate that for a real life dataset, our method performs better than a standard deep network, especially in hypoglycemic and hyperglycemic regimes. One noteworthy aspect of this work is that the training data and test data may come from different distributions.

A low discrepancy sequence on graphs

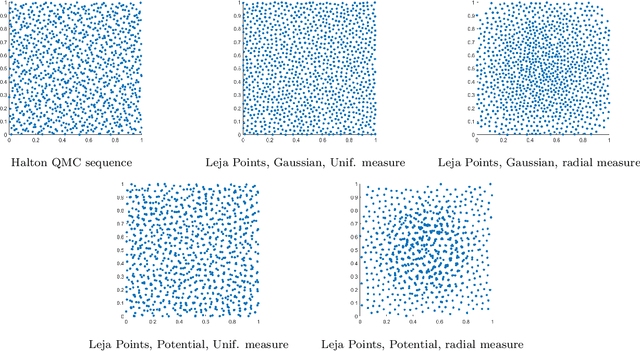
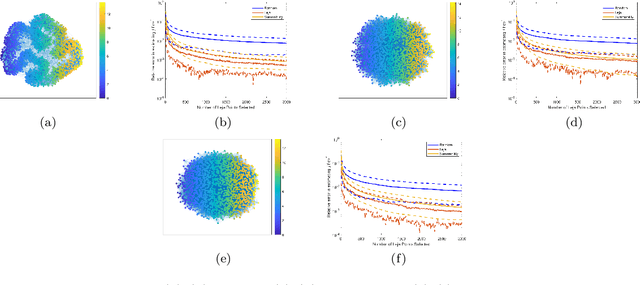
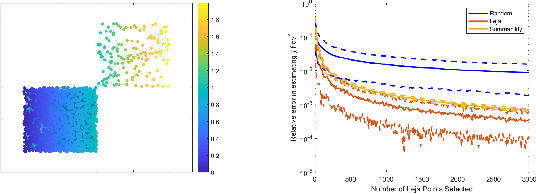
Many applications such as election forecasting, environmental monitoring, health policy, and graph based machine learning require taking expectation of functions defined on the vertices of a graph. We describe a construction of a sampling scheme analogous to the so called Leja points in complex potential theory that can be proved to give low discrepancy estimates for the approximation of the expected value by the impirical expected value based on these points. In contrast to classical potential theory where the kernel is fixed and the equilibrium distribution depends upon the kernel, we fix a probability distribution and construct a kernel (which represents the graph structure) for which the equilibrium distribution is the given probability distribution. Our estimates do not depend upon the size of the graph.

Super-resolution meets machine learning: approximation of measures

The problem of super-resolution in general terms is to recuperate a finitely supported measure $\mu$ given finitely many of its coefficients $\hat{\mu}(k)$ with respect to some orthonormal system. The interesting case concerns situations, where the number of coefficients required is substantially smaller than a power of the reciprocal of the minimal separation among the points in the support of $\mu$. In this paper, we consider the more severe problem of recuperating $\mu$ approximately without any assumption on $\mu$ beyond having a finite total variation. In particular, $\mu$ may be supported on a continuum, so that the minimal separation among the points in the support of $\mu$ is $0$. A variant of this problem is also of interest in machine learning as well as the inverse problem of de-convolution. We define an appropriate notion of a distance between the target measure and its recuperated version, give an explicit expression for the recuperation operator, and estimate the distance between $\mu$ and its approximation. We show that these estimates are the best possible in many different ways. We also explain why for a finitely supported measure the approximation quality of its recuperation is bounded from below if the amount of information is smaller than what is demanded in the super-resolution problem.

Function approximation by deep networks

We show that deep networks are better than shallow networks at approximating functions that can be expressed as a composition of functions described by a directed acyclic graph, because the deep networks can be designed to have the same compositional structure, while a shallow network cannot exploit this knowledge. Thus, the blessing of compositionality mitigates the curse of dimensionality. On the other hand, a theorem called good propagation of errors allows to `lift' theorems about shallow networks to those about deep networks with an appropriate choice of norms, smoothness, etc. We illustrate this in three contexts where each channel in the deep network calculates a spherical polynomial, a non-smooth ReLU network, or another zonal function network related closely with the ReLU network.

A witness function based construction of discriminative models using Hermite polynomials

In machine learning, we are given a dataset of the form $\{(\mathbf{x}_j,y_j)\}_{j=1}^M$, drawn as i.i.d. samples from an unknown probability distribution $\mu$; the marginal distribution for the $\mathbf{x}_j$'s being $\mu^*$. We propose that rather than using a positive kernel such as the Gaussian for estimation of these measures, using a non-positive kernel that preserves a large number of moments of these measures yields an optimal approximation. We use multi-variate Hermite polynomials for this purpose, and prove optimal and local approximation results in a supremum norm in a probabilistic sense. Together with a permutation test developed with the same kernel, we prove that the kernel estimator serves as a `witness function' in classification problems. Thus, if the value of this estimator at a point $\mathbf{x}$ exceeds a certain threshold, then the point is reliably in a certain class. This approach can be used to modify pretrained algorithms, such as neural networks or nonlinear dimension reduction techniques, to identify in-class vs out-of-class regions for the purposes of generative models, classification uncertainty, or finding robust centroids. This fact is demonstrated in a number of real world data sets including MNIST, CIFAR10, Science News documents, and LaLonde data sets.

A deep learning approach to diabetic blood glucose prediction

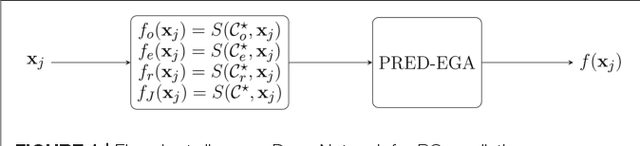
We consider the question of 30-minute prediction of blood glucose levels measured by continuous glucose monitoring devices, using clinical data. While most studies of this nature deal with one patient at a time, we take a certain percentage of patients in the data set as training data, and test on the remainder of the patients; i.e., the machine need not re-calibrate on the new patients in the data set. We demonstrate how deep learning can outperform shallow networks in this example. One novelty is to demonstrate how a parsimonious deep representation can be constructed using domain knowledge.

Deep nets for local manifold learning

The problem of extending a function $f$ defined on a training data $\mathcal{C}$ on an unknown manifold $\mathbb{X}$ to the entire manifold and a tubular neighborhood of this manifold is considered in this paper. For $\mathbb{X}$ embedded in a high dimensional ambient Euclidean space $\mathbb{R}^D$, a deep learning algorithm is developed for finding a local coordinate system for the manifold {\bf without eigen--decomposition}, which reduces the problem to the classical problem of function approximation on a low dimensional cube. Deep nets (or multilayered neural networks) are proposed to accomplish this approximation scheme by using the training data. Our methods do not involve such optimization techniques as back--propagation, while assuring optimal (a priori) error bounds on the output in terms of the number of derivatives of the target function. In addition, these methods are universal, in that they do not require a prior knowledge of the smoothness of the target function, but adjust the accuracy of approximation locally and automatically, depending only upon the local smoothness of the target function. Our ideas are easily extended to solve both the pre--image problem and the out--of--sample extension problem, with a priori bounds on the growth of the function thus extended.