A. Cloninger
A low discrepancy sequence on graphs
Oct 08, 2020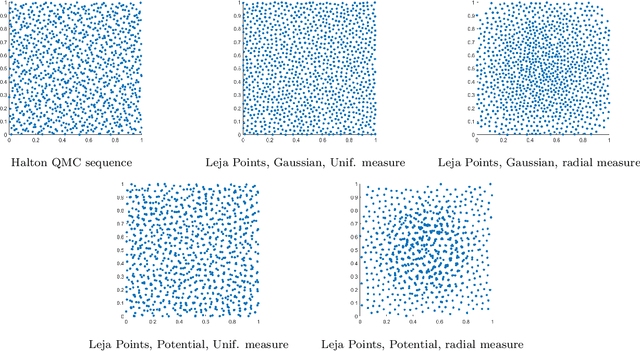
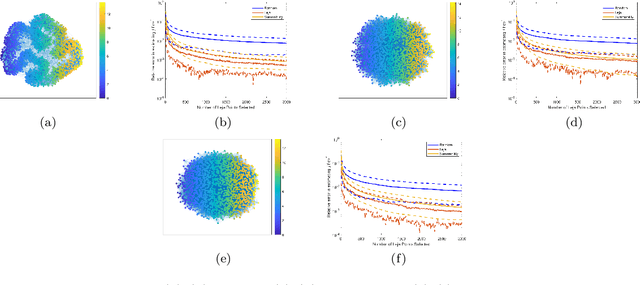
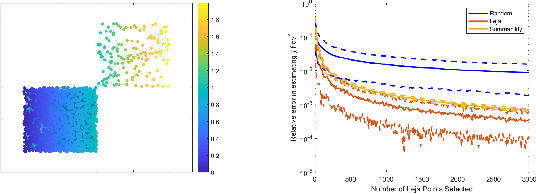

Abstract:Many applications such as election forecasting, environmental monitoring, health policy, and graph based machine learning require taking expectation of functions defined on the vertices of a graph. We describe a construction of a sampling scheme analogous to the so called Leja points in complex potential theory that can be proved to give low discrepancy estimates for the approximation of the expected value by the impirical expected value based on these points. In contrast to classical potential theory where the kernel is fixed and the equilibrium distribution depends upon the kernel, we fix a probability distribution and construct a kernel (which represents the graph structure) for which the equilibrium distribution is the given probability distribution. Our estimates do not depend upon the size of the graph.
A witness function based construction of discriminative models using Hermite polynomials
Jan 10, 2019



Abstract:In machine learning, we are given a dataset of the form $\{(\mathbf{x}_j,y_j)\}_{j=1}^M$, drawn as i.i.d. samples from an unknown probability distribution $\mu$; the marginal distribution for the $\mathbf{x}_j$'s being $\mu^*$. We propose that rather than using a positive kernel such as the Gaussian for estimation of these measures, using a non-positive kernel that preserves a large number of moments of these measures yields an optimal approximation. We use multi-variate Hermite polynomials for this purpose, and prove optimal and local approximation results in a supremum norm in a probabilistic sense. Together with a permutation test developed with the same kernel, we prove that the kernel estimator serves as a `witness function' in classification problems. Thus, if the value of this estimator at a point $\mathbf{x}$ exceeds a certain threshold, then the point is reliably in a certain class. This approach can be used to modify pretrained algorithms, such as neural networks or nonlinear dimension reduction techniques, to identify in-class vs out-of-class regions for the purposes of generative models, classification uncertainty, or finding robust centroids. This fact is demonstrated in a number of real world data sets including MNIST, CIFAR10, Science News documents, and LaLonde data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge