A low discrepancy sequence on graphs
Paper and Code
Oct 08, 2020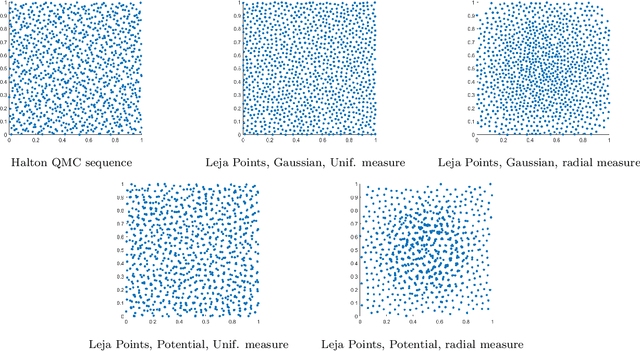
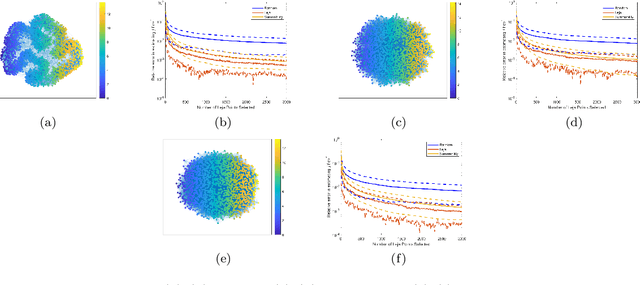
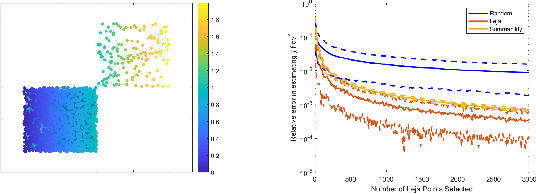

Many applications such as election forecasting, environmental monitoring, health policy, and graph based machine learning require taking expectation of functions defined on the vertices of a graph. We describe a construction of a sampling scheme analogous to the so called Leja points in complex potential theory that can be proved to give low discrepancy estimates for the approximation of the expected value by the impirical expected value based on these points. In contrast to classical potential theory where the kernel is fixed and the equilibrium distribution depends upon the kernel, we fix a probability distribution and construct a kernel (which represents the graph structure) for which the equilibrium distribution is the given probability distribution. Our estimates do not depend upon the size of the graph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge