M. D. van der Walt
A function approximation approach to the prediction of blood glucose levels
May 12, 2021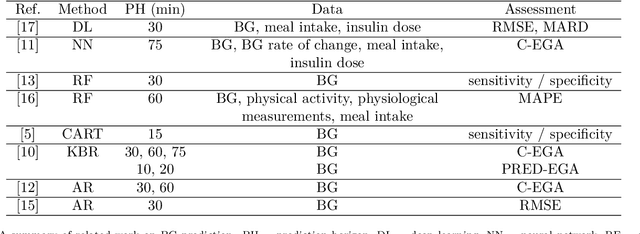



Abstract:The problem of real time prediction of blood glucose (BG) levels based on the readings from a continuous glucose monitoring (CGM) device is a problem of great importance in diabetes care, and therefore, has attracted a lot of research in recent years, especially based on machine learning. An accurate prediction with a 30, 60, or 90 minute prediction horizon has the potential of saving millions of dollars in emergency care costs. In this paper, we treat the problem as one of function approximation, where the value of the BG level at time $t+h$ (where $h$ the prediction horizon) is considered to be an unknown function of $d$ readings prior to the time $t$. This unknown function may be supported in particular on some unknown submanifold of the $d$-dimensional Euclidean space. While manifold learning is classically done in a semi-supervised setting, where the entire data has to be known in advance, we use recent ideas to achieve an accurate function approximation in a supervised setting; i.e., construct a model for the target function. We use the state-of-the-art clinically relevant PRED-EGA grid to evaluate our results, and demonstrate that for a real life dataset, our method performs better than a standard deep network, especially in hypoglycemic and hyperglycemic regimes. One noteworthy aspect of this work is that the training data and test data may come from different distributions.
A deep learning approach to diabetic blood glucose prediction
Jul 18, 2017



Abstract:We consider the question of 30-minute prediction of blood glucose levels measured by continuous glucose monitoring devices, using clinical data. While most studies of this nature deal with one patient at a time, we take a certain percentage of patients in the data set as training data, and test on the remainder of the patients; i.e., the machine need not re-calibrate on the new patients in the data set. We demonstrate how deep learning can outperform shallow networks in this example. One novelty is to demonstrate how a parsimonious deep representation can be constructed using domain knowledge.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge