Robust and tractable multidimensional exponential analysis

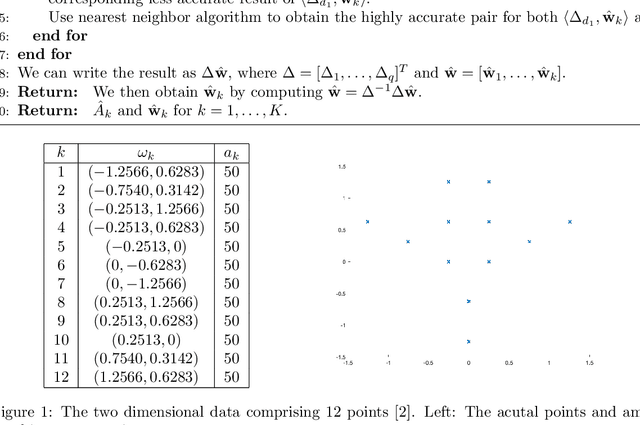
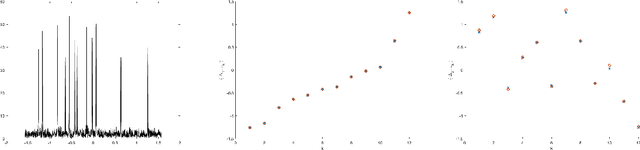
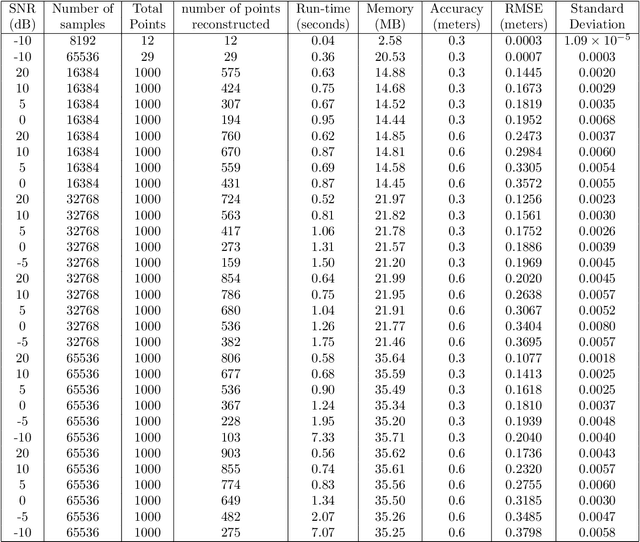
Motivated by a number of applications in signal processing, we study the following question. Given samples of a multidimensional signal of the form \begin{align*} f(\bs\ell)=\sum_{k=1}^K a_k\exp(-i\langle \bs\ell, \w_k\rangle), \\ \w_1,\cdots,\w_k\in\mathbb{R}^q, \ \bs\ell\in \ZZ^q, \ |\bs\ell| <n, \end{align*} determine the values of the number $K$ of components, and the parameters $a_k$ and $\w_k$'s. We develop an algorithm to recuperate these quantities accurately using only a subsample of size $\O(qn)$ of this data. For this purpose, we use a novel localized kernel method to identify the parameters, including the number $K$ of signals. Our method is easy to implement, and is shown to be stable under a very low SNR range. We demonstrate the effectiveness of our resulting algorithm using 2 and 3 dimensional examples from the literature, and show substantial improvements over state-of-the-art techniques including Prony based, MUSIC and ESPRIT approaches.