Fast Stochastic Hierarchical Bayesian MAP for Tomographic Imaging
Paper and Code
Jul 07, 2017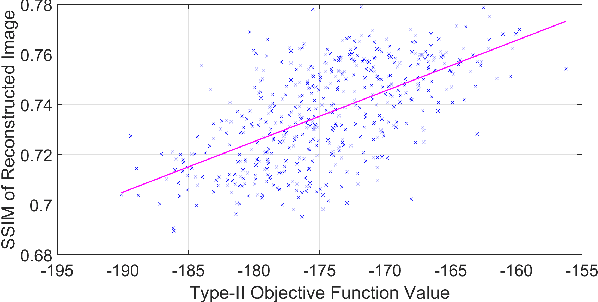
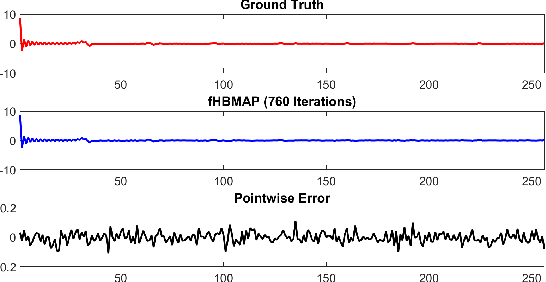
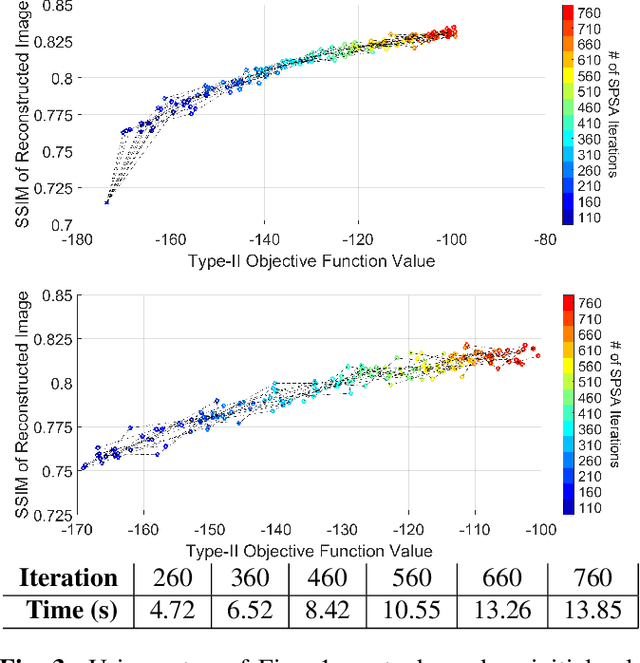
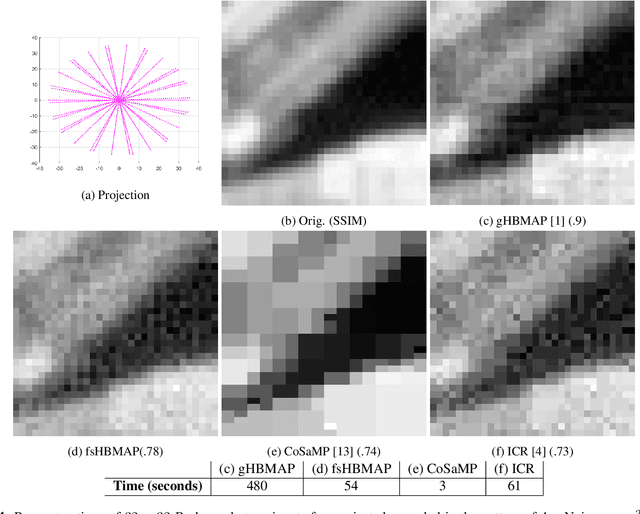
Any image recovery algorithm attempts to achieve the highest quality reconstruction in a timely manner. The former can be achieved in several ways, among which are by incorporating Bayesian priors that exploit natural image tendencies to cue in on relevant phenomena. The Hierarchical Bayesian MAP (HB-MAP) is one such approach which is known to produce compelling results albeit at a substantial computational cost. We look to provide further analysis and insights into what makes the HB-MAP work. While retaining the proficient nature of HB-MAP's Type-I estimation, we propose a stochastic approximation-based approach to Type-II estimation. The resulting algorithm, fast stochastic HB-MAP (fsHBMAP), takes dramatically fewer operations while retaining high reconstruction quality. We employ our fsHBMAP scheme towards the problem of tomographic imaging and demonstrate that fsHBMAP furnishes promising results when compared to many competing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge