EdgeConvFormer: Dynamic Graph CNN and Transformer based Anomaly Detection in Multivariate Time Series

Transformer-based models for anomaly detection in multivariate time series can benefit from the self-attention mechanism due to its advantage in modeling long-term dependencies. However, Transformer-based anomaly detection models have problems such as a large amount of data being required for training, standard positional encoding is not suitable for multivariate time series data, and the interdependence between time series is not considered. To address these limitations, we propose a novel anomaly detection method, named EdgeConvFormer, which integrates Time2vec embedding, stacked dynamic graph CNN, and Transformer to extract global and local spatial-time information. This design of EdgeConvFormer empowers it with decomposition capacities for complex time series, progressive spatiotemporal correlation discovery between time series, and representation aggregation of multi-scale features. Experiments demonstrate that EdgeConvFormer can learn the spatial-temporal correlations from multivariate time series data and achieve better anomaly detection performance than the state-of-the-art approaches on many real-world datasets of different scales.

A Novel Exploration of Diffusion Process based on Multi-types Galton-Watson Forests

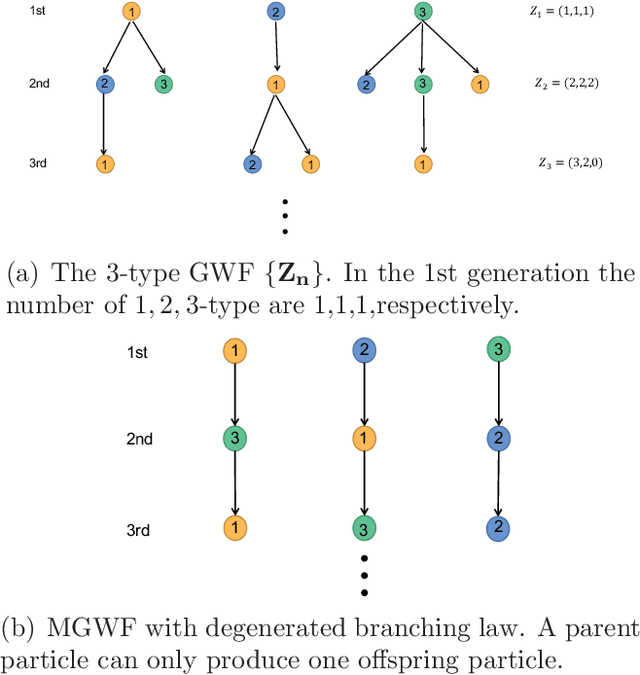
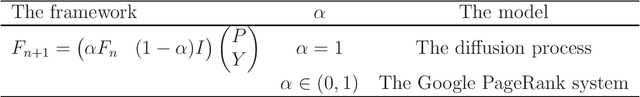
Diffusion is a commonly used technique for spreading information from point to point on a graph. The rationale behind diffusion is not clear. And the multi-types Galton-Watson forest is a random model of population growth without space or any other resource constraints. In this paper, we use the degenerated multi-types Galton-Watson forest (MGWF) to interpret the diffusion process and establish an equivalent relationship between them. With the two-phase setting of the MGWF, one can interpret the diffusion process and the Google PageRank system explicitly. It also improves the convergence behaviour of the iterative diffusion process and Google PageRank system. We validate the proposal by experiment while providing new research directions.

Regularizing Semi-supervised Graph Convolutional Networks with a Manifold Smoothness Loss

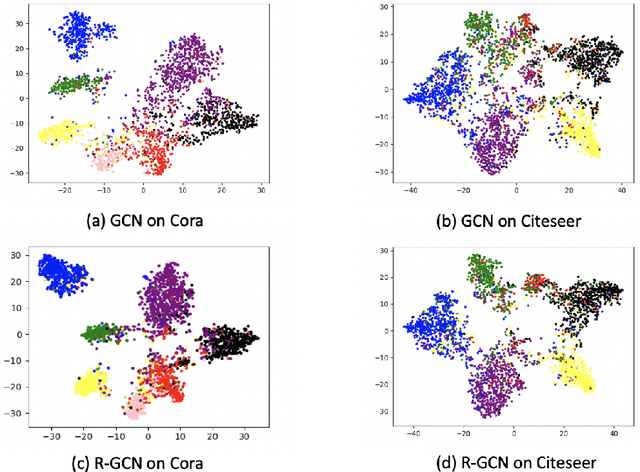
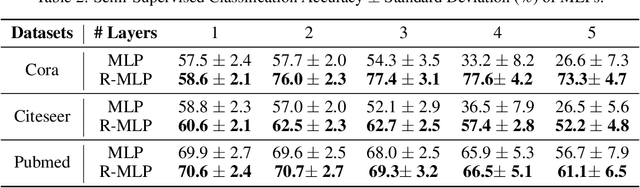
Existing graph convolutional networks focus on the neighborhood aggregation scheme. When applied to semi-supervised learning, they often suffer from the overfitting problem as the networks are trained with the cross-entropy loss on a small potion of labeled data. In this paper, we propose an unsupervised manifold smoothness loss defined with respect to the graph structure, which can be added to the loss function as a regularization. We draw connections between the proposed loss with an iterative diffusion process, and show that minimizing the loss is equivalent to aggregate neighbor predictions with infinite layers. We conduct experiments on multi-layer perceptron and existing graph networks, and demonstrate that adding the proposed loss can improve the performance consistently.

Semi-supervised Learning on Graph with an Alternating Diffusion Process

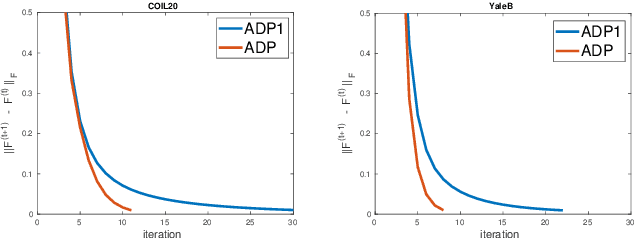
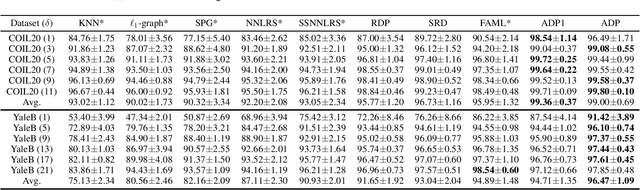
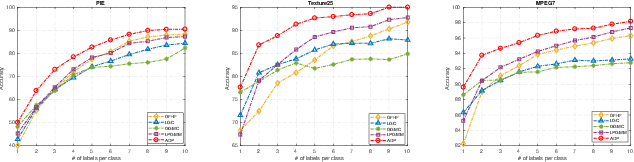
Graph-based semi-supervised learning usually involves two separate stages, constructing an affinity graph and then propagating labels for transductive inference on the graph. It is suboptimal to solve them independently, as the correlation between the affinity graph and labels are not fully exploited. In this paper, we integrate the two stages into one unified framework by formulating the graph construction as a regularized function estimation problem similar to label propagation. We propose an alternating diffusion process to solve the two problems simultaneously, which allows us to learn the graph and unknown labels in an iterative fashion. With the proposed framework, we are able to adequately leverage both the given labels and estimated labels to construct a better graph, and effectively propagate labels on such a dynamic graph updated simultaneously with the newly obtained labels. Extensive experiments on various real-world datasets have demonstrated the superiority of the proposed method compared to other state-of-the-art methods.

Sparse Subspace Clustering via Diffusion Process

Subspace clustering refers to the problem of clustering high-dimensional data that lie in a union of low-dimensional subspaces. State-of-the-art subspace clustering methods are based on the idea of expressing each data point as a linear combination of other data points while regularizing the matrix of coefficients with L1, L2 or nuclear norms for a sparse solution. L1 regularization is guaranteed to give a subspace-preserving affinity (i.e., there are no connections between points from different subspaces) under broad theoretical conditions, but the clusters may not be fully connected. L2 and nuclear norm regularization often improve connectivity, but give a subspace-preserving affinity only for independent subspaces. Mixed L1, L2 and nuclear norm regularization could offer a balance between the subspace-preserving and connectedness properties, but this comes at the cost of increased computational complexity. This paper focuses on using L1 norm and alleviating the corresponding connectivity problem by a simple yet efficient diffusion process on subspace affinity graphs. Without adding any tuning parameter , our method can achieve state-of-the-art clustering performance on Hopkins 155 and Extended Yale B data sets.