Semi-supervised Learning on Graph with an Alternating Diffusion Process
Paper and Code
Feb 16, 2019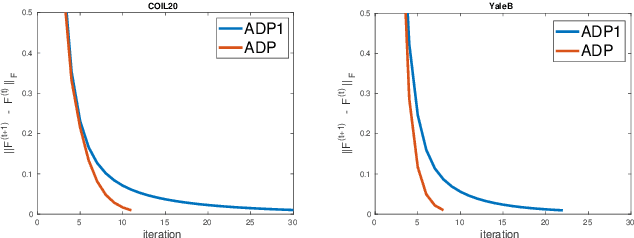
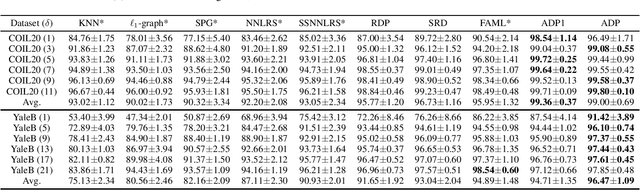
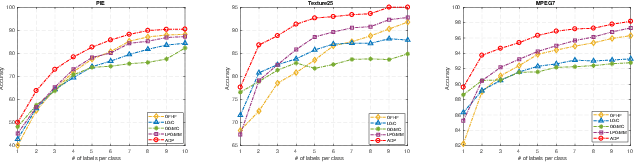

Graph-based semi-supervised learning usually involves two separate stages, constructing an affinity graph and then propagating labels for transductive inference on the graph. It is suboptimal to solve them independently, as the correlation between the affinity graph and labels are not fully exploited. In this paper, we integrate the two stages into one unified framework by formulating the graph construction as a regularized function estimation problem similar to label propagation. We propose an alternating diffusion process to solve the two problems simultaneously, which allows us to learn the graph and unknown labels in an iterative fashion. With the proposed framework, we are able to adequately leverage both the given labels and estimated labels to construct a better graph, and effectively propagate labels on such a dynamic graph updated simultaneously with the newly obtained labels. Extensive experiments on various real-world datasets have demonstrated the superiority of the proposed method compared to other state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge