Regularizing Semi-supervised Graph Convolutional Networks with a Manifold Smoothness Loss
Paper and Code
Feb 11, 2020

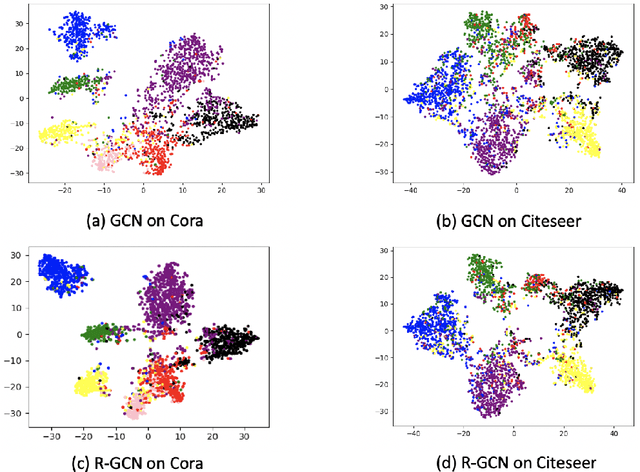
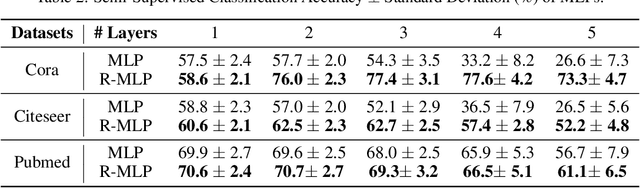
Existing graph convolutional networks focus on the neighborhood aggregation scheme. When applied to semi-supervised learning, they often suffer from the overfitting problem as the networks are trained with the cross-entropy loss on a small potion of labeled data. In this paper, we propose an unsupervised manifold smoothness loss defined with respect to the graph structure, which can be added to the loss function as a regularization. We draw connections between the proposed loss with an iterative diffusion process, and show that minimizing the loss is equivalent to aggregate neighbor predictions with infinite layers. We conduct experiments on multi-layer perceptron and existing graph networks, and demonstrate that adding the proposed loss can improve the performance consistently.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge