A Novel Exploration of Diffusion Process based on Multi-types Galton-Watson Forests

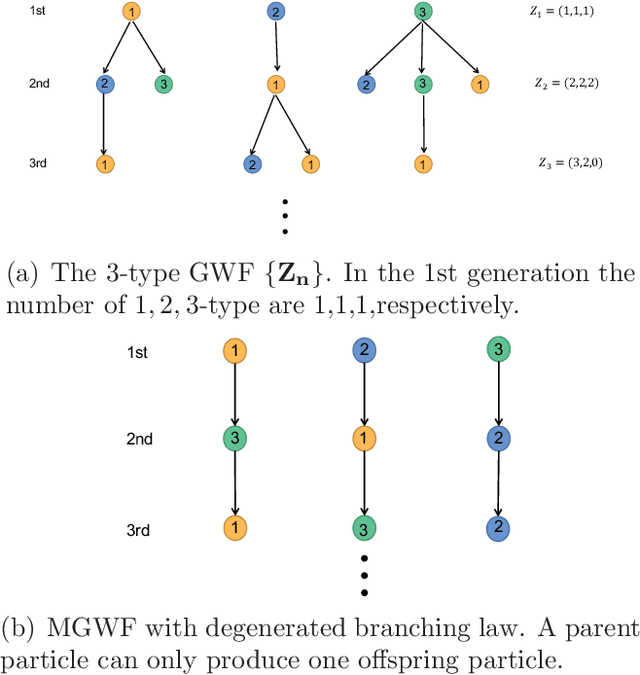
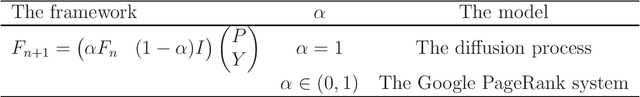
Diffusion is a commonly used technique for spreading information from point to point on a graph. The rationale behind diffusion is not clear. And the multi-types Galton-Watson forest is a random model of population growth without space or any other resource constraints. In this paper, we use the degenerated multi-types Galton-Watson forest (MGWF) to interpret the diffusion process and establish an equivalent relationship between them. With the two-phase setting of the MGWF, one can interpret the diffusion process and the Google PageRank system explicitly. It also improves the convergence behaviour of the iterative diffusion process and Google PageRank system. We validate the proposal by experiment while providing new research directions.

Elliptical Distributions-Based Weights-Determining Method for OWA Operators

The ordered weighted averaging (OWA) operators play a crucial role in aggregating multiple criteria evaluations into an overall assessment supporting the decision makers' choice. One key point steps is to determine the associated weights. In this paper, we first briefly review some main methods for determining the weights by using distribution functions. Then we propose a new approach for determining OWA weights by using the RIM quantifier. Motivated by the idea of normal distribution-based method to determine the OWA weights, we develop a method based on elliptical distributions for determining the OWA weights, and some of its desirable properties have been investigated.