Qianqian Ma
Finite-Sample Analysis of Decentralized Q-Learning for Stochastic Games
Dec 16, 2021



Abstract:Learning in stochastic games is arguably the most standard and fundamental setting in multi-agent reinforcement learning (MARL). In this paper, we consider decentralized MARL in stochastic games in the non-asymptotic regime. In particular, we establish the finite-sample complexity of fully decentralized Q-learning algorithms in a significant class of general-sum stochastic games (SGs) - weakly acyclic SGs, which includes the common cooperative MARL setting with an identical reward to all agents (a Markov team problem) as a special case. We focus on the practical while challenging setting of fully decentralized MARL, where neither the rewards nor the actions of other agents can be observed by each agent. In fact, each agent is completely oblivious to the presence of other decision makers. Both the tabular and the linear function approximation cases have been considered. In the tabular setting, we analyze the sample complexity for the decentralized Q-learning algorithm to converge to a Markov perfect equilibrium (Nash equilibrium). With linear function approximation, the results are for convergence to a linear approximated equilibrium - a new notion of equilibrium that we propose - which describes that each agent's policy is a best reply (to other agents) within a linear space. Numerical experiments are also provided for both settings to demonstrate the results.
Semi-supervised Domain Adaptive Structure Learning
Dec 12, 2021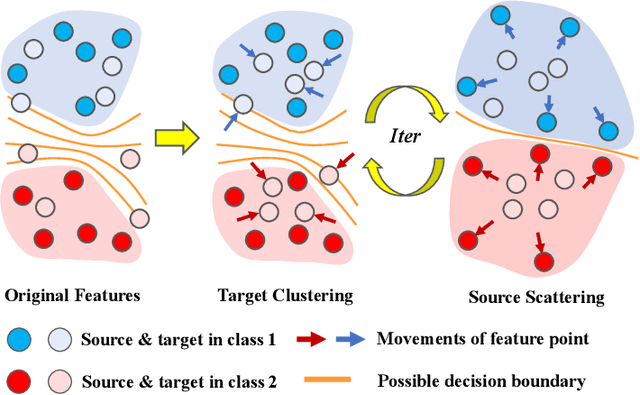
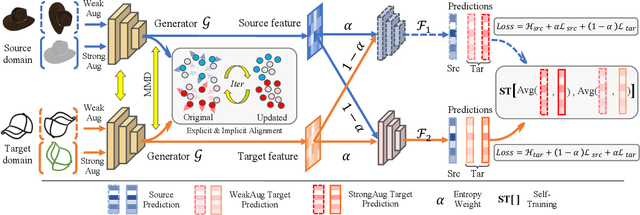
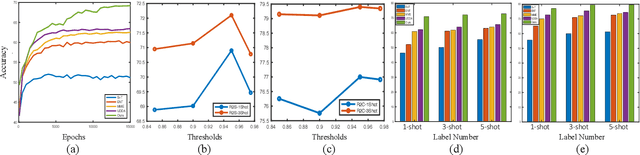

Abstract:Semi-supervised domain adaptation (SSDA) is quite a challenging problem requiring methods to overcome both 1) overfitting towards poorly annotated data and 2) distribution shift across domains. Unfortunately, a simple combination of domain adaptation (DA) and semi-supervised learning (SSL) methods often fail to address such two objects because of training data bias towards labeled samples. In this paper, we introduce an adaptive structure learning method to regularize the cooperation of SSL and DA. Inspired by the multi-views learning, our proposed framework is composed of a shared feature encoder network and two classifier networks, trained for contradictory purposes. Among them, one of the classifiers is applied to group target features to improve intra-class density, enlarging the gap of categorical clusters for robust representation learning. Meanwhile, the other classifier, serviced as a regularizer, attempts to scatter the source features to enhance the smoothness of the decision boundary. The iterations of target clustering and source expansion make the target features being well-enclosed inside the dilated boundary of the corresponding source points. For the joint address of cross-domain features alignment and partially labeled data learning, we apply the maximum mean discrepancy (MMD) distance minimization and self-training (ST) to project the contradictory structures into a shared view to make the reliable final decision. The experimental results over the standard SSDA benchmarks, including DomainNet and Office-home, demonstrate both the accuracy and robustness of our method over the state-of-the-art approaches.
Adversarial Crowdsourcing Through Robust Rank-One Matrix Completion
Oct 23, 2020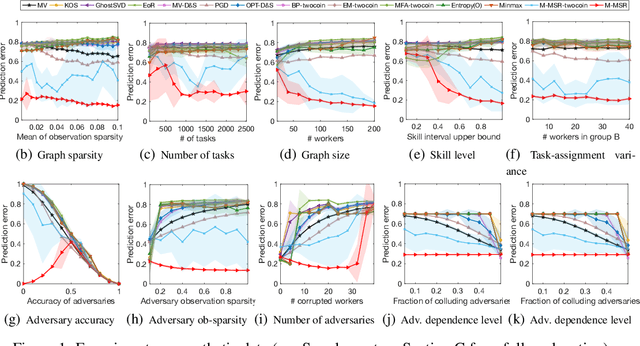
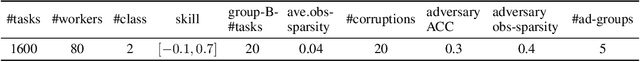
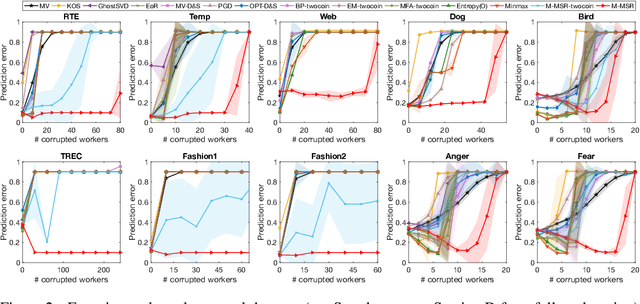

Abstract:We consider the problem of reconstructing a rank-one matrix from a revealed subset of its entries when some of the revealed entries are corrupted with perturbations that are unknown and can be arbitrarily large. It is not known which revealed entries are corrupted. We propose a new algorithm combining alternating minimization with extreme-value filtering and provide sufficient and necessary conditions to recover the original rank-one matrix. In particular, we show that our proposed algorithm is optimal when the set of revealed entries is given by an Erd\H{o}s-R\'enyi random graph. These results are then applied to the problem of classification from crowdsourced data under the assumption that while the majority of the workers are governed by the standard single-coin David-Skene model (i.e., they output the correct answer with a certain probability), some of the workers can deviate arbitrarily from this model. In particular, the "adversarial" workers could even make decisions designed to make the algorithm output an incorrect answer. Extensive experimental results show our algorithm for this problem, based on rank-one matrix completion with perturbations, outperforms all other state-of-the-art methods in such an adversarial scenario.
Opposite Structure Learning for Semi-supervised Domain Adaptation
Feb 06, 2020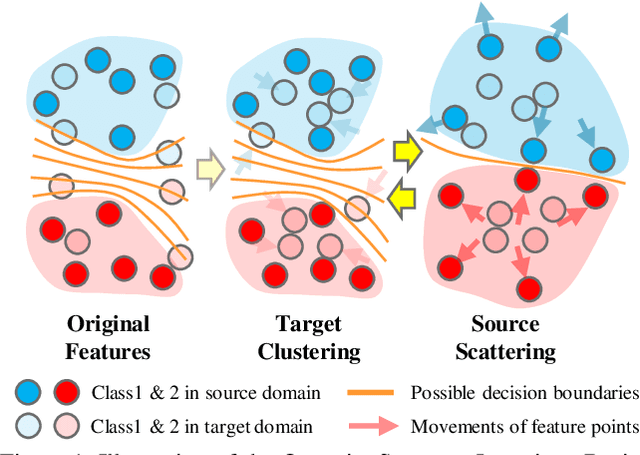

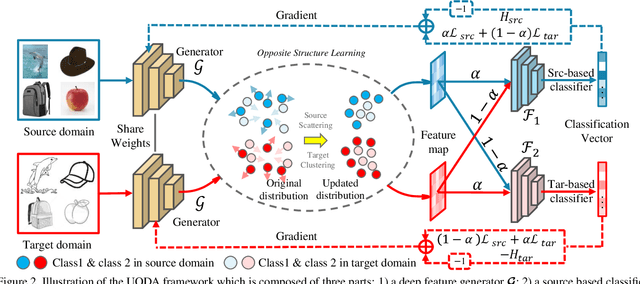

Abstract:Current adversarial adaptation methods attempt to align the cross-domain features whereas two challenges remain unsolved: 1) conditional distribution mismatch between different domains and 2) the bias of decision boundary towards the source domain. To solve these challenges, we propose a novel framework for semi-supervised domain adaptation by unifying the learning of opposite structures (UODA). UODA consists of a generator and two classifiers (i.e., the source-based and the target-based classifiers respectively) which are trained with opposite forms of losses for a unified object. The target-based classifier attempts to cluster the target features to improve intra-class density and enlarge inter-class divergence. Meanwhile, the source-based classifier is designed to scatter the source features to enhance the smoothness of decision boundary. Through the alternation of source-feature expansion and target-feature clustering procedures, the target features are well-enclosed within the dilated boundary of the corresponding source features. This strategy effectively makes the cross-domain features precisely aligned. To overcome the model collapse through training, we progressively update the measurement of distance and the feature representation on both domains via an adversarial training paradigm. Extensive experiments on the benchmarks of DomainNet and Office-home datasets demonstrate the effectiveness of our approach over the state-of-the-art method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge