Adversarial Crowdsourcing Through Robust Rank-One Matrix Completion
Paper and Code
Oct 23, 2020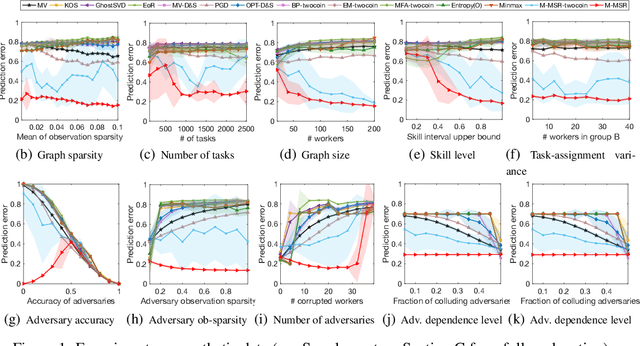
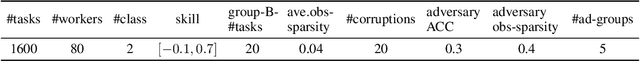
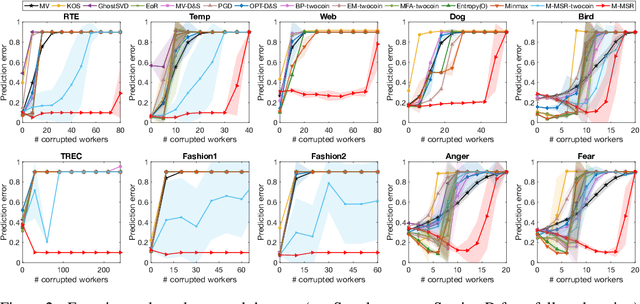

We consider the problem of reconstructing a rank-one matrix from a revealed subset of its entries when some of the revealed entries are corrupted with perturbations that are unknown and can be arbitrarily large. It is not known which revealed entries are corrupted. We propose a new algorithm combining alternating minimization with extreme-value filtering and provide sufficient and necessary conditions to recover the original rank-one matrix. In particular, we show that our proposed algorithm is optimal when the set of revealed entries is given by an Erd\H{o}s-R\'enyi random graph. These results are then applied to the problem of classification from crowdsourced data under the assumption that while the majority of the workers are governed by the standard single-coin David-Skene model (i.e., they output the correct answer with a certain probability), some of the workers can deviate arbitrarily from this model. In particular, the "adversarial" workers could even make decisions designed to make the algorithm output an incorrect answer. Extensive experimental results show our algorithm for this problem, based on rank-one matrix completion with perturbations, outperforms all other state-of-the-art methods in such an adversarial scenario.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge