Enabling Group Fairness in Graph Unlearning via Bi-level Debiasing

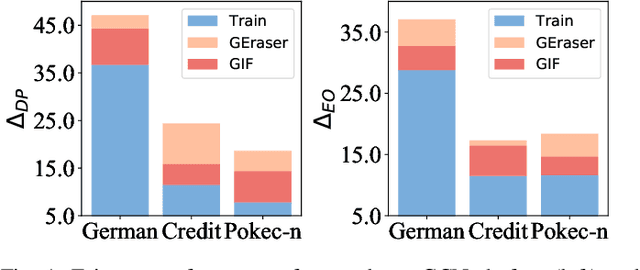
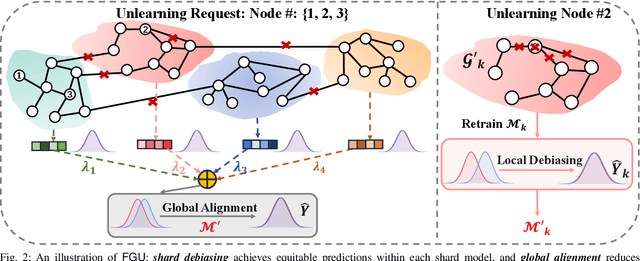
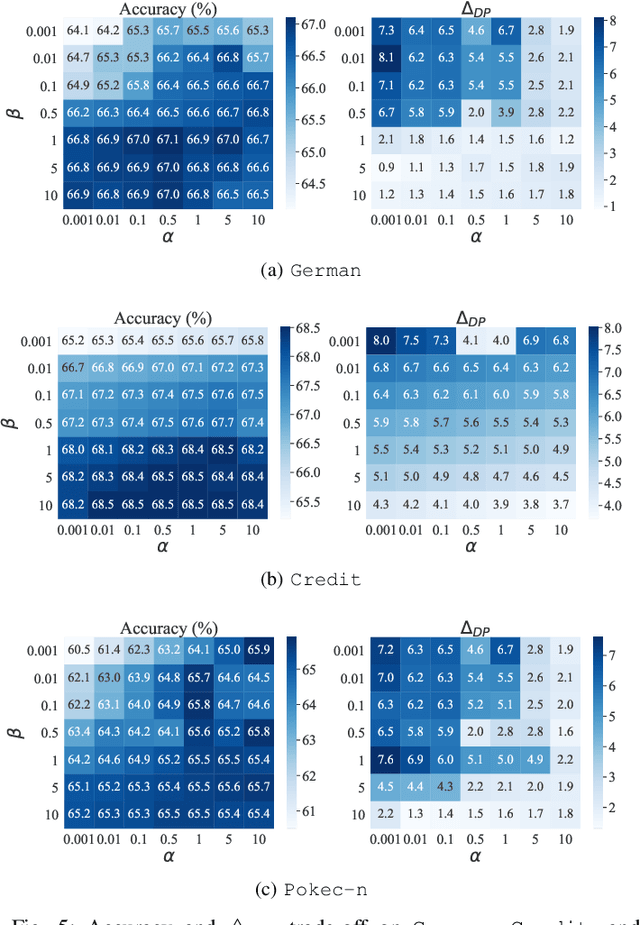
Graph unlearning is a crucial approach for protecting user privacy by erasing the influence of user data on trained graph models. Recent developments in graph unlearning methods have primarily focused on maintaining model prediction performance while removing user information. However, we have observed that when user information is deleted from the model, the prediction distribution across different sensitive groups often changes. Furthermore, graph models are shown to be prone to amplifying biases, making the study of fairness in graph unlearning particularly important. This raises the question: Does graph unlearning actually introduce bias? Our findings indicate that the predictions of post-unlearning models become highly correlated with sensitive attributes, confirming the introduction of bias in the graph unlearning process. To address this issue, we propose a fair graph unlearning method, FGU. To guarantee privacy, FGU trains shard models on partitioned subgraphs, unlearns the requested data from the corresponding subgraphs, and retrains the shard models on the modified subgraphs. To ensure fairness, FGU employs a bi-level debiasing process: it first enables shard-level fairness by incorporating a fairness regularizer in the shard model retraining, and then achieves global-level fairness by aligning all shard models to minimize global disparity. Our experiments demonstrate that FGU achieves superior fairness while maintaining privacy and accuracy. Additionally, FGU is robust to diverse unlearning requests, ensuring fairness and utility performance across various data distributions.

Hyperdimensional Quantum Factorization

This paper presents a quantum algorithm for efficiently decoding hypervectors, a crucial process in extracting atomic elements from hypervectors - an essential task in Hyperdimensional Computing (HDC) models for interpretable learning and information retrieval. HDC employs high-dimensional vectors and efficient operators to encode and manipulate information, representing complex objects from atomic concepts. When one attempts to decode a hypervector that is the product (binding) of multiple hypervectors, the factorization becomes prohibitively costly with classical optimization-based methods and specialized recurrent networks, an inherent consequence of the binding operation. We propose HDQF, an innovative quantum computing approach, to address this challenge. By exploiting parallels between HDC and quantum computing and capitalizing on quantum algorithms' speedup capabilities, HDQF encodes potential factors as a quantum superposition using qubit states and bipolar vector representation. This yields a quadratic speedup over classical search methods and effectively mitigates Hypervector Factorization capacity issues.

Self-Attention Based Semantic Decomposition in Vector Symbolic Architectures

Vector Symbolic Architectures (VSAs) have emerged as a novel framework for enabling interpretable machine learning algorithms equipped with the ability to reason and explain their decision processes. The basic idea is to represent discrete information through high dimensional random vectors. Complex data structures can be built up with operations over vectors such as the "binding" operation involving element-wise vector multiplication, which associates data together. The reverse task of decomposing the associated elements is a combinatorially hard task, with an exponentially large search space. The main algorithm for performing this search is the resonator network, inspired by Hopfield network-based memory search operations. In this work, we introduce a new variant of the resonator network, based on self-attention based update rules in the iterative search problem. This update rule, based on the Hopfield network with log-sum-exp energy function and norm-bounded states, is shown to substantially improve the performance and rate of convergence. As a result, our algorithm enables a larger capacity for associative memory, enabling applications in many tasks like perception based pattern recognition, scene decomposition, and object reasoning. We substantiate our algorithm with a thorough evaluation and comparisons to baselines.