The WILDTRACK Multi-Camera Person Dataset

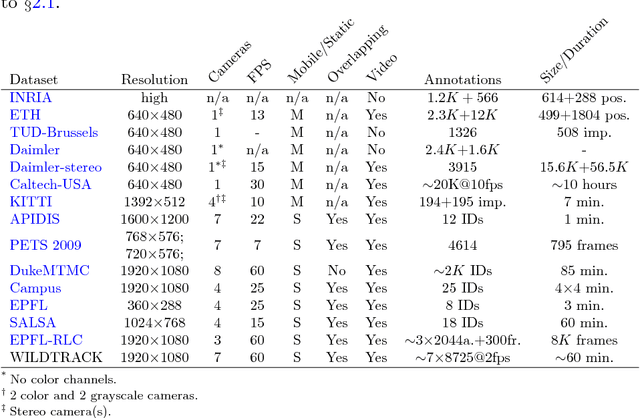
People detection methods are highly sensitive to the perpetual occlusions among the targets. As multi-camera set-ups become more frequently encountered, joint exploitation of the across views information would allow for improved detection performances. We provide a large-scale HD dataset named WILDTRACK which finally makes advanced deep learning methods applicable to this problem. The seven-static-camera set-up captures realistic and challenging scenarios of walking people. Notably, its camera calibration with jointly high-precision projection widens the range of algorithms which may make use of this dataset. In aim to help accelerate the research on automatic camera calibration, such annotations also accompany this dataset. Furthermore, the rich-in-appearance visual context of the pedestrian class makes this dataset attractive for monocular pedestrian detection as well, since: the HD cameras are placed relatively close to the people, and the size of the dataset further increases seven-fold. In summary, we overview existing multi-camera datasets and detection methods, enumerate details of our dataset, and we benchmark multi-camera state of the art detectors on this new dataset.

Deep Occlusion Reasoning for Multi-Camera Multi-Target Detection

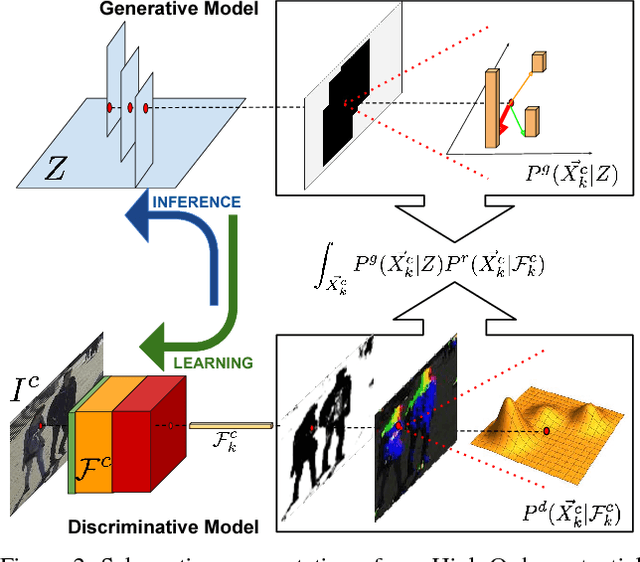
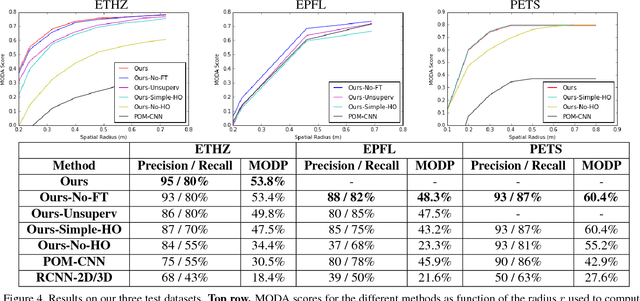
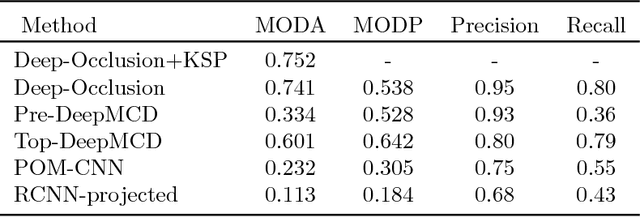
People detection in single 2D images has improved greatly in recent years. However, comparatively little of this progress has percolated into multi-camera multi-people tracking algorithms, whose performance still degrades severely when scenes become very crowded. In this work, we introduce a new architecture that combines Convolutional Neural Nets and Conditional Random Fields to explicitly model those ambiguities. One of its key ingredients are high-order CRF terms that model potential occlusions and give our approach its robustness even when many people are present. Our model is trained end-to-end and we show that it outperforms several state-of-art algorithms on challenging scenes.

Multi-Modal Mean-Fields via Cardinality-Based Clamping

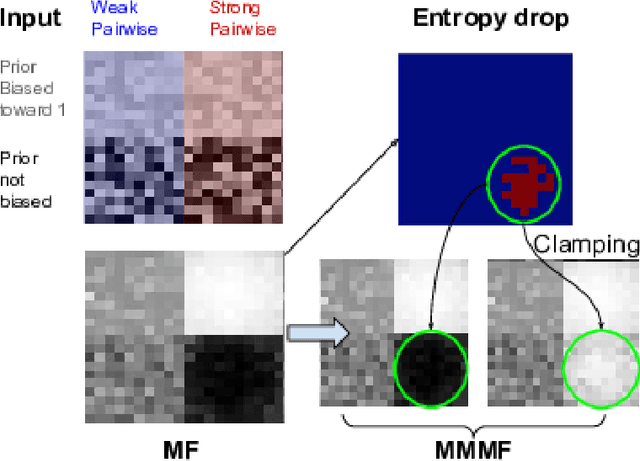
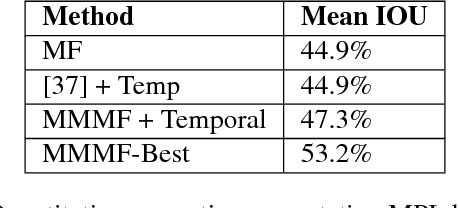
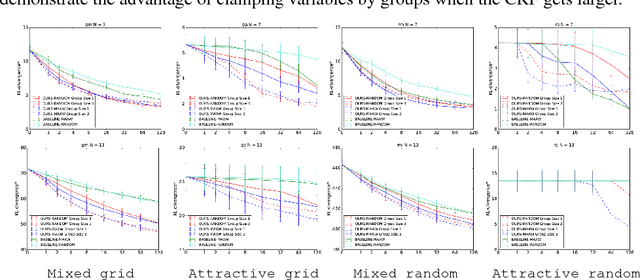
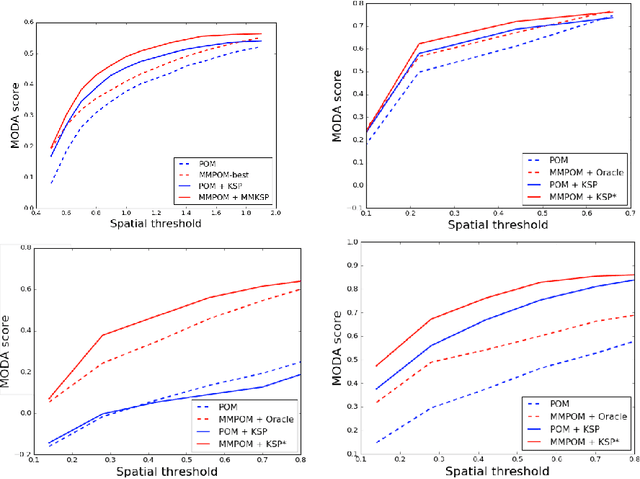
Mean Field inference is central to statistical physics. It has attracted much interest in the Computer Vision community to efficiently solve problems expressible in terms of large Conditional Random Fields. However, since it models the posterior probability distribution as a product of marginal probabilities, it may fail to properly account for important dependencies between variables. We therefore replace the fully factorized distribution of Mean Field by a weighted mixture of such distributions, that similarly minimizes the KL-Divergence to the true posterior. By introducing two new ideas, namely, conditioning on groups of variables instead of single ones and using a parameter of the conditional random field potentials, that we identify to the temperature in the sense of statistical physics to select such groups, we can perform this minimization efficiently. Our extension of the clamping method proposed in previous works allows us to both produce a more descriptive approximation of the true posterior and, inspired by the diverse MAP paradigms, fit a mixture of Mean Field approximations. We demonstrate that this positively impacts real-world algorithms that initially relied on mean fields.

Principled Parallel Mean-Field Inference for Discrete Random Fields

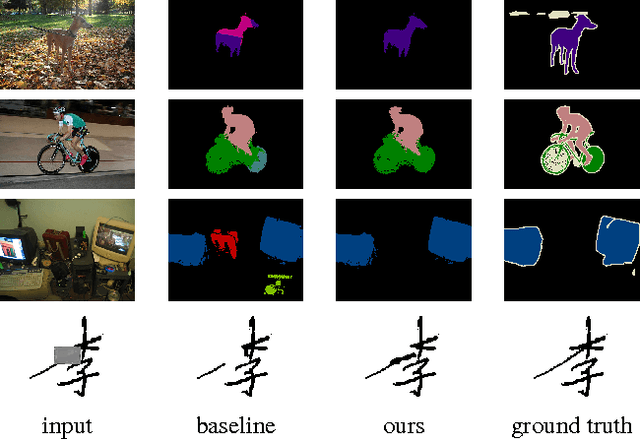
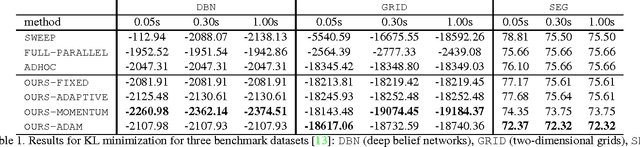
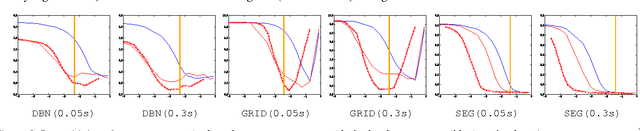
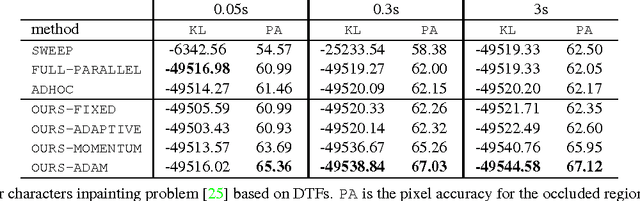
Mean-field variational inference is one of the most popular approaches to inference in discrete random fields. Standard mean-field optimization is based on coordinate descent and in many situations can be impractical. Thus, in practice, various parallel techniques are used, which either rely on ad-hoc smoothing with heuristically set parameters, or put strong constraints on the type of models. In this paper, we propose a novel proximal gradient-based approach to optimizing the variational objective. It is naturally parallelizable and easy to implement. We prove its convergence, and then demonstrate that, in practice, it yields faster convergence and often finds better optima than more traditional mean-field optimization techniques. Moreover, our method is less sensitive to the choice of parameters.

A provably convergent alternating minimization method for mean field inference

Mean-Field is an efficient way to approximate a posterior distribution in complex graphical models and constitutes the most popular class of Bayesian variational approximation methods. In most applications, the mean field distribution parameters are computed using an alternate coordinate minimization. However, the convergence properties of this algorithm remain unclear. In this paper, we show how, by adding an appropriate penalization term, we can guarantee convergence to a critical point, while keeping a closed form update at each step. A convergence rate estimate can also be derived based on recent results in non-convex optimization.