The AI Agent Index

Leading AI developers and startups are increasingly deploying agentic AI systems that can plan and execute complex tasks with limited human involvement. However, there is currently no structured framework for documenting the technical components, intended uses, and safety features of agentic systems. To fill this gap, we introduce the AI Agent Index, the first public database to document information about currently deployed agentic AI systems. For each system that meets the criteria for inclusion in the index, we document the system's components (e.g., base model, reasoning implementation, tool use), application domains (e.g., computer use, software engineering), and risk management practices (e.g., evaluation results, guardrails), based on publicly available information and correspondence with developers. We find that while developers generally provide ample information regarding the capabilities and applications of agentic systems, they currently provide limited information regarding safety and risk management practices. The AI Agent Index is available online at https://aiagentindex.mit.edu/

Learning Symbolic Representations for Reinforcement Learning of Non-Markovian Behavior

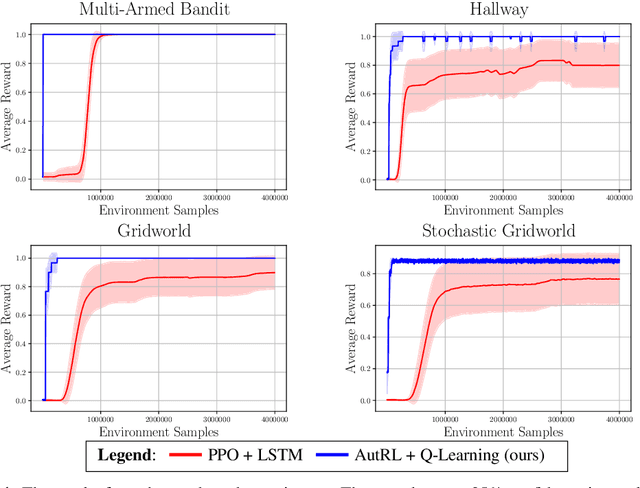
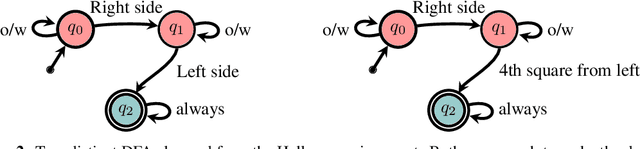
Many real-world reinforcement learning (RL) problems necessitate learning complex, temporally extended behavior that may only receive reward signal when the behavior is completed. If the reward-worthy behavior is known, it can be specified in terms of a non-Markovian reward function - a function that depends on aspects of the state-action history, rather than just the current state and action. Such reward functions yield sparse rewards, necessitating an inordinate number of experiences to find a policy that captures the reward-worthy pattern of behavior. Recent work has leveraged Knowledge Representation (KR) to provide a symbolic abstraction of aspects of the state that summarize reward-relevant properties of the state-action history and support learning a Markovian decomposition of the problem in terms of an automaton over the KR. Providing such a decomposition has been shown to vastly improve learning rates, especially when coupled with algorithms that exploit automaton structure. Nevertheless, such techniques rely on a priori knowledge of the KR. In this work, we explore how to automatically discover useful state abstractions that support learning automata over the state-action history. The result is an end-to-end algorithm that can learn optimal policies with significantly fewer environment samples than state-of-the-art RL on simple non-Markovian domains.

Get It in Writing: Formal Contracts Mitigate Social Dilemmas in Multi-Agent RL

Multi-agent reinforcement learning (MARL) is a powerful tool for training automated systems acting independently in a common environment. However, it can lead to sub-optimal behavior when individual incentives and group incentives diverge. Humans are remarkably capable at solving these social dilemmas. It is an open problem in MARL to replicate such cooperative behaviors in selfish agents. In this work, we draw upon the idea of formal contracting from economics to overcome diverging incentives between agents in MARL. We propose an augmentation to a Markov game where agents voluntarily agree to binding state-dependent transfers of reward, under pre-specified conditions. Our contributions are theoretical and empirical. First, we show that this augmentation makes all subgame-perfect equilibria of all fully observed Markov games exhibit socially optimal behavior, given a sufficiently rich space of contracts. Next, we complement our game-theoretic analysis by showing that state-of-the-art RL algorithms learn socially optimal policies given our augmentation. Our experiments include classic static dilemmas like Stag Hunt, Prisoner's Dilemma and a public goods game, as well as dynamic interactions that simulate traffic, pollution management and common pool resource management.