Multi-Objective Decision Transformers for Offline Reinforcement Learning

Offline Reinforcement Learning (RL) is structured to derive policies from static trajectory data without requiring real-time environment interactions. Recent studies have shown the feasibility of framing offline RL as a sequence modeling task, where the sole aim is to predict actions based on prior context using the transformer architecture. However, the limitation of this single task learning approach is its potential to undermine the transformer model's attention mechanism, which should ideally allocate varying attention weights across different tokens in the input context for optimal prediction. To address this, we reformulate offline RL as a multi-objective optimization problem, where the prediction is extended to states and returns. We also highlight a potential flaw in the trajectory representation used for sequence modeling, which could generate inaccuracies when modeling the state and return distributions. This is due to the non-smoothness of the action distribution within the trajectory dictated by the behavioral policy. To mitigate this issue, we introduce action space regions to the trajectory representation. Our experiments on D4RL benchmark locomotion tasks reveal that our propositions allow for more effective utilization of the attention mechanism in the transformer model, resulting in performance that either matches or outperforms current state-of-the art methods.

Neural network approaches to point lattice decoding

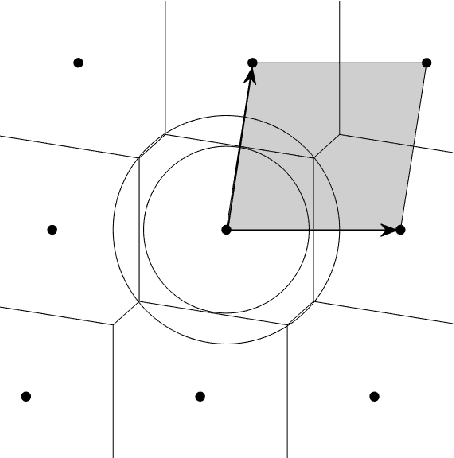
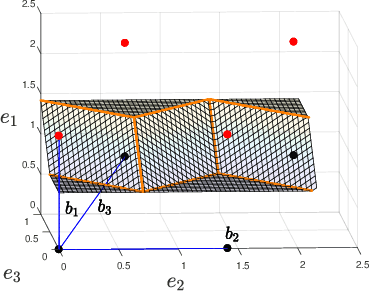
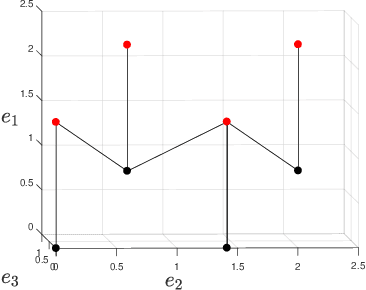
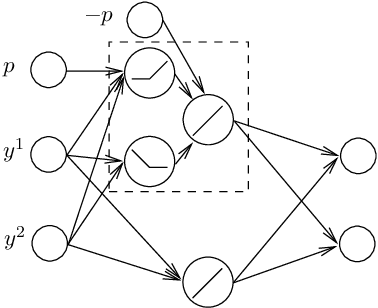
We characterize the complexity of the lattice decoding problem from a neural network perspective. The notion of Voronoi-reduced basis is introduced to restrict the space of solutions to a binary set. On the one hand, this problem is shown to be equivalent to computing a continuous piecewise linear (CPWL) function restricted to the fundamental parallelotope. On the other hand, it is known that any function computed by a ReLU feed-forward neural network is CPWL. As a result, we count the number of affine pieces in the CPWL decoding function to characterize the complexity of the decoding problem. It is exponential in the space dimension $n$, which induces shallow neural networks of exponential size. For structured lattices we show that folding, a technique equivalent to using a deep neural network, enables to reduce this complexity from exponential in $n$ to polynomial in $n$. Regarding unstructured MIMO lattices, in contrary to dense lattices many pieces in the CPWL decoding function can be neglected for quasi-optimal decoding on the Gaussian channel. This makes the decoding problem easier and it explains why shallow neural networks of reasonable size are more efficient with this category of lattices (in low to moderate dimensions).

Deep Reinforcement Learning for Wireless Scheduling with Multiclass Services

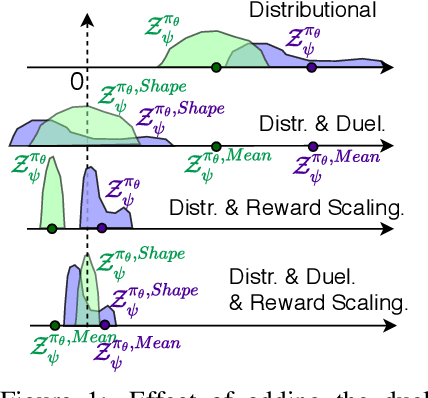
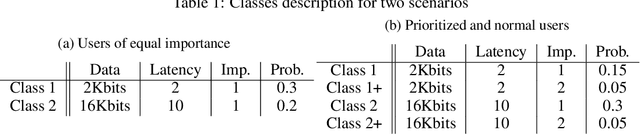
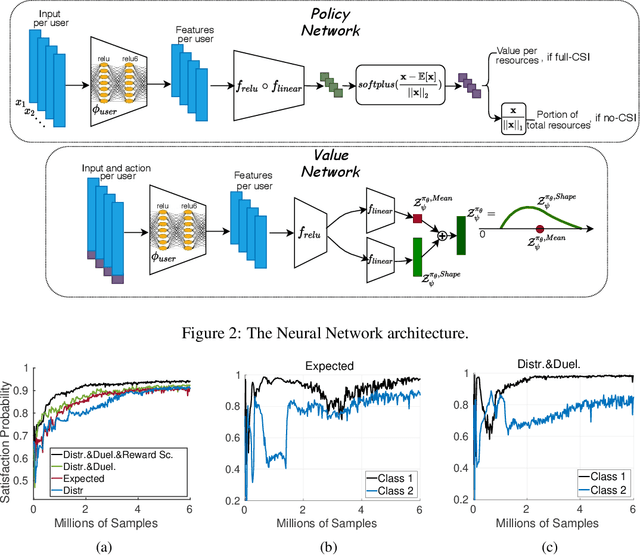
In this paper, we investigate the problem of scheduling and resource allocation over a time varying set of clients with heterogeneous demands.In this context, a service provider has to schedule traffic destined to users with different classes of requirements and to allocate bandwidth resources over time as a means to efficiently satisfy service demands within a limited time horizon. This is a highly intricate problem, in particular in wireless communication systems, and solutions may involve tools stemming from diverse fields, including combinatorics and constrained optimization. Although recent work has successfully proposed solutions based on Deep Reinforcement Learning (DRL), the challenging setting of heterogeneous user traffic and demands has not been addressed. We propose a deep deterministic policy gradient algorithm that combines state-of-the-art techniques, namely Distributional RL and Deep Sets, to train a model for heterogeneous traffic scheduling. We test on diverse scenarios with different time dependence dynamics, users' requirements, and resources available, demonstrating consistent results using both synthetic and real data. We evaluate the algorithm on a wireless communication setting using both synthetic and real data and show significant gains in terms of Quality of Service (QoS) defined by the classes, against state-of-the-art conventional algorithms from combinatorics, optimization and scheduling metric(e.g. Knapsack, Integer Linear Programming, Frank-Wolfe, Exponential Rule).

GraphCL: Contrastive Self-Supervised Learning of Graph Representations

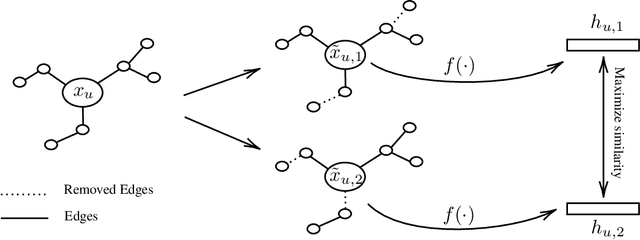
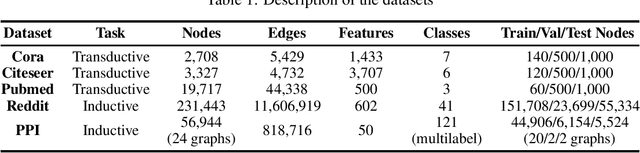
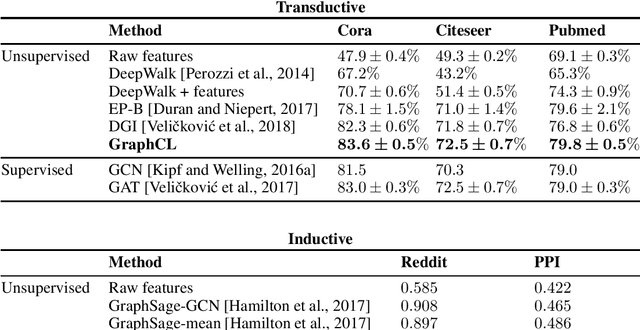
We propose Graph Contrastive Learning (GraphCL), a general framework for learning node representations in a self supervised manner. GraphCL learns node embeddings by maximizing the similarity between the representations of two randomly perturbed versions of the intrinsic features and link structure of the same node's local subgraph. We use graph neural networks to produce two representations of the same node and leverage a contrastive learning loss to maximize agreement between them. In both transductive and inductive learning setups, we demonstrate that our approach significantly outperforms the state-of-the-art in unsupervised learning on a number of node classification benchmarks.

A lattice-based approach to the expressivity of deep ReLU neural networks

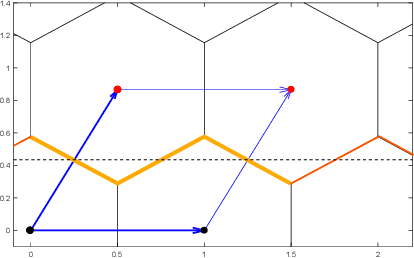
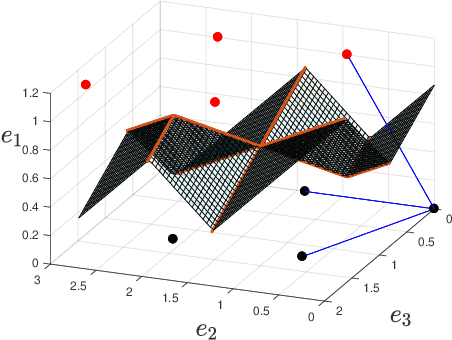
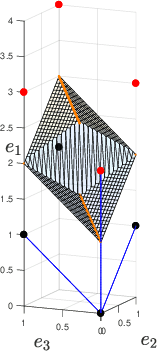
We present new families of continuous piecewise linear (CPWL) functions in Rn having a number of affine pieces growing exponentially in $n$. We show that these functions can be seen as the high-dimensional generalization of the triangle wave function used by Telgarsky in 2016. We prove that they can be computed by ReLU networks with quadratic depth and linear width in the space dimension. We also investigate the approximation error of one of these functions by shallower networks and prove a separation result. The main difference between our functions and other constructions is their practical interest: they arise in the scope of channel coding. Hence, computing such functions amounts to performing a decoding operation.

On the CVP for the root lattices via folding with deep ReLU neural networks

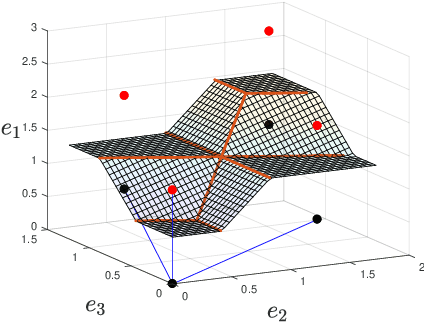
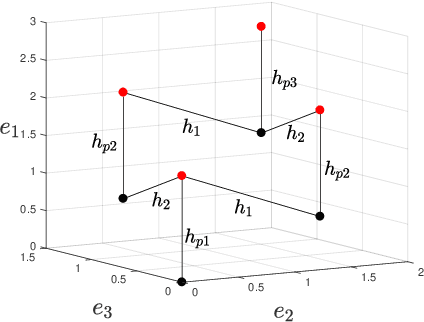
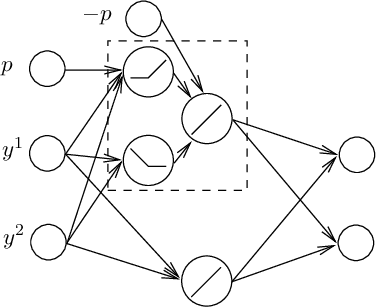
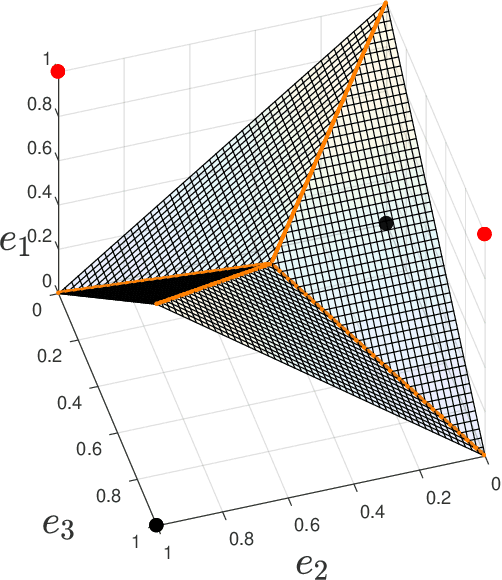
Point lattices and their decoding via neural networks are considered in this paper. Lattice decoding in Rn, known as the closest vector problem (CVP), becomes a classification problem in the fundamental parallelotope with a piecewise linear function defining the boundary. Theoretical results are obtained by studying root lattices. We show how the number of pieces in the boundary function reduces dramatically with folding, from exponential to linear. This translates into a two-layer ReLU network requiring a number of neurons growing exponentially in n to solve the CVP, whereas this complexity becomes polynomial in n for a deep ReLU network.