Neural network approaches to point lattice decoding

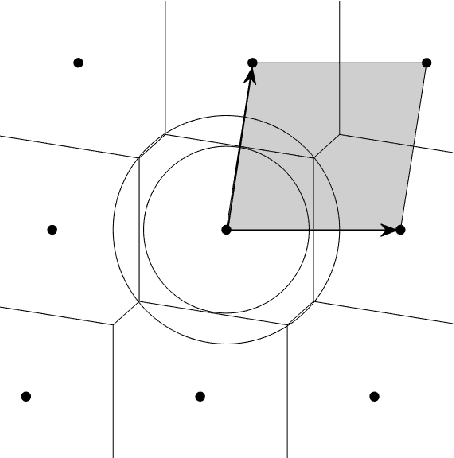
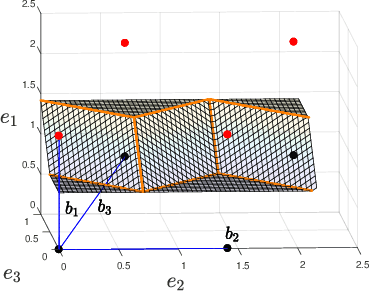
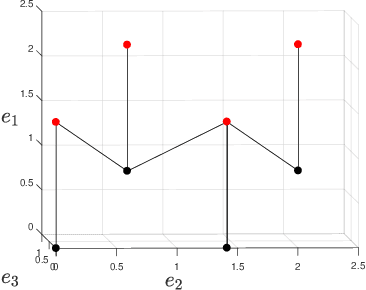
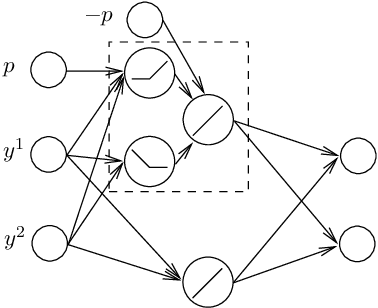
We characterize the complexity of the lattice decoding problem from a neural network perspective. The notion of Voronoi-reduced basis is introduced to restrict the space of solutions to a binary set. On the one hand, this problem is shown to be equivalent to computing a continuous piecewise linear (CPWL) function restricted to the fundamental parallelotope. On the other hand, it is known that any function computed by a ReLU feed-forward neural network is CPWL. As a result, we count the number of affine pieces in the CPWL decoding function to characterize the complexity of the decoding problem. It is exponential in the space dimension $n$, which induces shallow neural networks of exponential size. For structured lattices we show that folding, a technique equivalent to using a deep neural network, enables to reduce this complexity from exponential in $n$ to polynomial in $n$. Regarding unstructured MIMO lattices, in contrary to dense lattices many pieces in the CPWL decoding function can be neglected for quasi-optimal decoding on the Gaussian channel. This makes the decoding problem easier and it explains why shallow neural networks of reasonable size are more efficient with this category of lattices (in low to moderate dimensions).

A lattice-based approach to the expressivity of deep ReLU neural networks

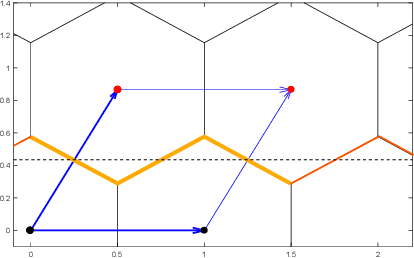
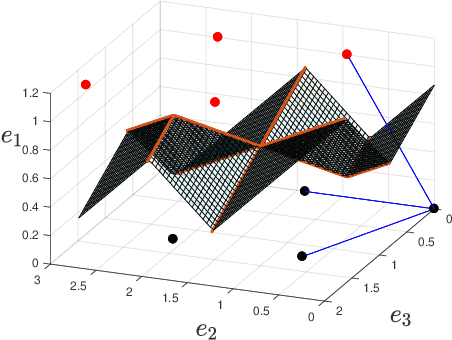
We present new families of continuous piecewise linear (CPWL) functions in Rn having a number of affine pieces growing exponentially in $n$. We show that these functions can be seen as the high-dimensional generalization of the triangle wave function used by Telgarsky in 2016. We prove that they can be computed by ReLU networks with quadratic depth and linear width in the space dimension. We also investigate the approximation error of one of these functions by shallower networks and prove a separation result. The main difference between our functions and other constructions is their practical interest: they arise in the scope of channel coding. Hence, computing such functions amounts to performing a decoding operation.

On the CVP for the root lattices via folding with deep ReLU neural networks

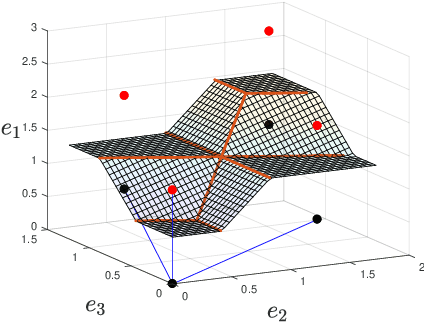
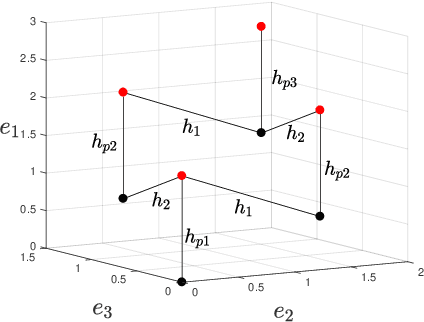
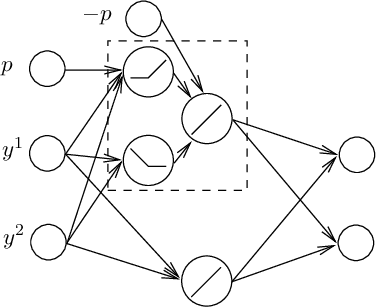
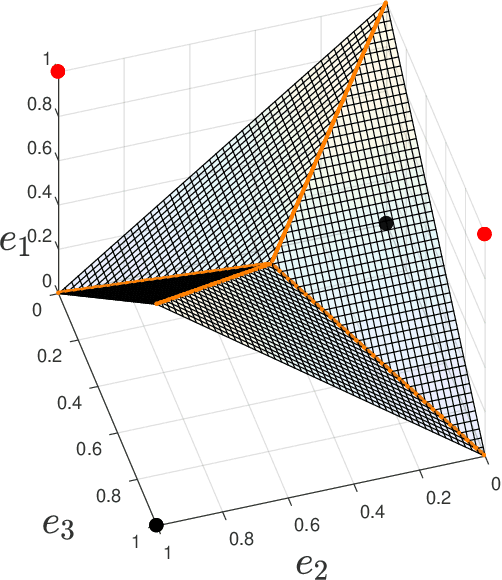
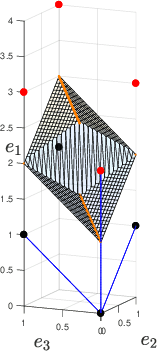
Point lattices and their decoding via neural networks are considered in this paper. Lattice decoding in Rn, known as the closest vector problem (CVP), becomes a classification problem in the fundamental parallelotope with a piecewise linear function defining the boundary. Theoretical results are obtained by studying root lattices. We show how the number of pieces in the boundary function reduces dramatically with folding, from exponential to linear. This translates into a two-layer ReLU network requiring a number of neurons growing exponentially in n to solve the CVP, whereas this complexity becomes polynomial in n for a deep ReLU network.