Beyond Tree Models: A Hybrid Model of KAN and gMLP for Large-Scale Financial Tabular Data

Tabular data plays a critical role in real-world financial scenarios. Traditionally, tree models have dominated in handling tabular data. However, financial datasets in the industry often encounter some challenges, such as data heterogeneity, the predominance of numerical features and the large scale of the data, which can range from tens of millions to hundreds of millions of records. These challenges can lead to significant memory and computational issues when using tree-based models. Consequently, there is a growing need for neural network-based solutions that can outperform these models. In this paper, we introduce TKGMLP, an hybrid network for tabular data that combines shallow Kolmogorov Arnold Networks with Gated Multilayer Perceptron. This model leverages the strengths of both architectures to improve performance and scalability. We validate TKGMLP on a real-world credit scoring dataset, where it achieves state-of-the-art results and outperforms current benchmarks. Furthermore, our findings demonstrate that the model continues to improve as the dataset size increases, making it highly scalable. Additionally, we propose a novel feature encoding method for numerical data, specifically designed to address the predominance of numerical features in financial datasets. The integration of this feature encoding method within TKGMLP significantly improves prediction accuracy. This research not only advances table prediction technology but also offers a practical and effective solution for handling large-scale numerical tabular data in various industrial applications.

Ultra-imbalanced classification guided by statistical information

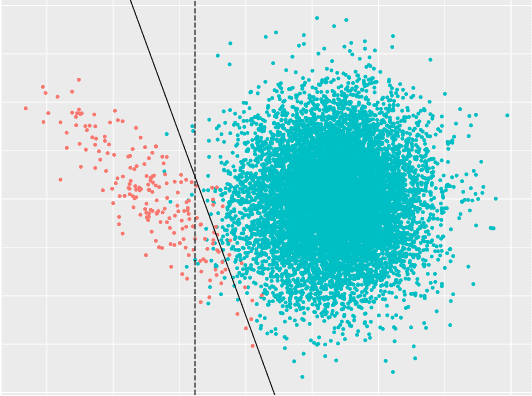
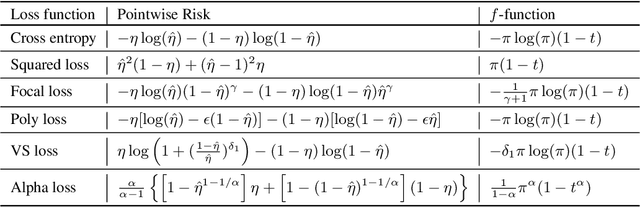
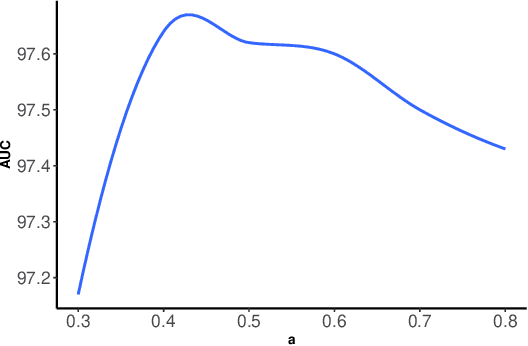
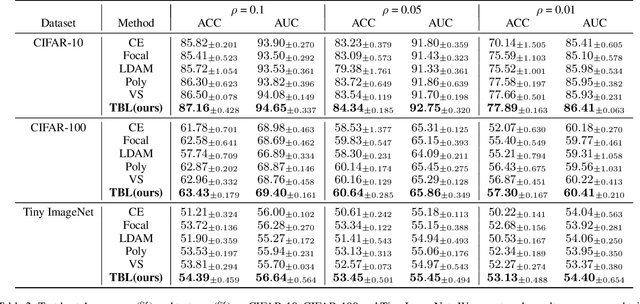
Imbalanced data are frequently encountered in real-world classification tasks. Previous works on imbalanced learning mostly focused on learning with a minority class of few samples. However, the notion of imbalance also applies to cases where the minority class contains abundant samples, which is usually the case for industrial applications like fraud detection in the area of financial risk management. In this paper, we take a population-level approach to imbalanced learning by proposing a new formulation called \emph{ultra-imbalanced classification} (UIC). Under UIC, loss functions behave differently even if infinite amount of training samples are available. To understand the intrinsic difficulty of UIC problems, we borrow ideas from information theory and establish a framework to compare different loss functions through the lens of statistical information. A novel learning objective termed Tunable Boosting Loss is developed which is provably resistant against data imbalance under UIC, as well as being empirically efficient verified by extensive experimental studies on both public and industrial datasets.