Pavithra Prabhakar
Formal Modeling and Verification of Publisher-Subscriber Paradigm in ROS 2
Dec 12, 2024Abstract:The Robot Operating System (ROS) is one of the most popular middleware for developing robot applications, but it is subject to major shortcomings when applied to real-time robotic systems in safety-critical environments. For this reason, ROS 2 was released in 2017 for implementing real-time capabilities in distributed robotic systems while supporting the most prominent aspects of the original ROS. There is still not much work done to provide formal guarantees and correctness of a ROS program. In this paper, we propose a framework to address this challenging problem of guaranteeing the correct behaviour of robotic systems. We propose a formal modelling of a ROS 2 program, and also describe the program using a network of timed automata. We then prove that the sets of executions of a ROS program in the model and in the network of timed automata are the same. Thus to analyze a publisher-subscriber scenario of ROS 2 program, our algorithm first converts the program into the model, and then into the network of timed automata. The applicability and validity of our approach are verified by conducting several experiments on a simplified system and an actual robotic system, and the results and limitations are discussed.
Abstraction-based Probabilistic Stability Analysis of Polyhedral Probabilistic Hybrid Systems
Mar 29, 2023Abstract:In this paper, we consider the problem of probabilistic stability analysis of a subclass of Stochastic Hybrid Systems, namely, Polyhedral Probabilistic Hybrid Systems (PPHS), where the flow dynamics is given by a polyhedral inclusion, the discrete switching between modes happens probabilistically at the boundaries of their invariant regions and the continuous state is not reset during switching. We present an abstraction-based analysis framework that consists of constructing a finite Markov Decision Processes (MDP) such that verification of certain property on the finite MDP ensures the satisfaction of probabilistic stability on the PPHS. Further, we present a polynomial-time algorithm for verifying the corresponding property on the MDP. Our experimental analysis demonstrates the feasibility of the approach in successfully verifying probabilistic stability on PPHS of various dimensions and sizes.
Bayesian Statistical Model Checking for Multi-agent Systems using HyperPCTL*
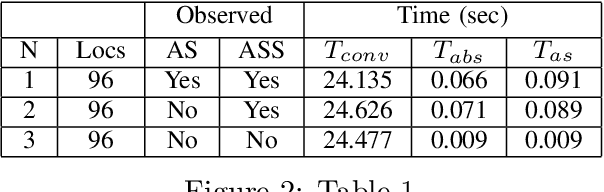
Sep 06, 2022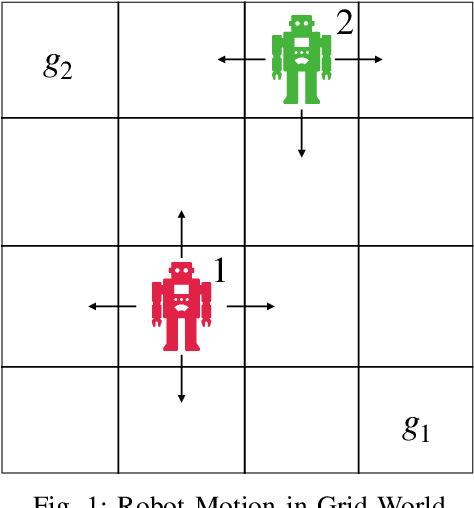
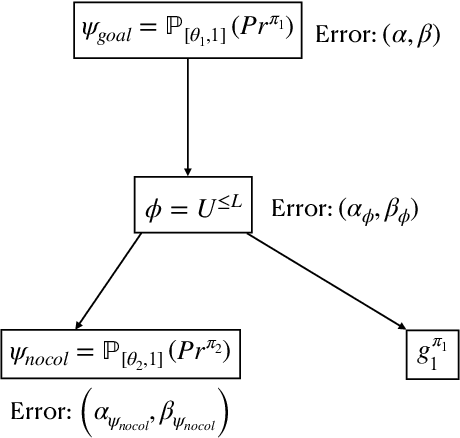


Abstract:In this paper, we present a Bayesian method for statistical model checking (SMC) of probabilistic hyperproperties specified in the logic HyperPCTL* on discrete-time Markov chains (DTMCs). While SMC of HyperPCTL* using sequential probability ratio test (SPRT) has been explored before, we develop an alternative SMC algorithm based on Bayesian hypothesis testing. In comparison to PCTL*, verifying HyperPCTL* formulae is complex owing to their simultaneous interpretation on multiple paths of the DTMC. In addition, extending the bottom-up model-checking algorithm of the non-probabilistic setting is not straight forward due to the fact that SMC does not return exact answers to the satisfiability problems of subformulae, instead, it only returns correct answers with high-confidence. We propose a recursive algorithm for SMC of HyperPCTL* based on a modified Bayes' test that factors in the uncertainty in the recursive satisfiability results. We have implemented our algorithm in a Python toolbox, HyProVer, and compared our approach with the SPRT based SMC. Our experimental evaluation demonstrates that our Bayesian SMC algorithm performs better both in terms of the verification time and the number of samples required to deduce satisfiability of a given HyperPCTL* formula.
Probabilistic Stability Analysis of Planar Robots with Piecewise Constant Derivative Dynamics
Oct 08, 2021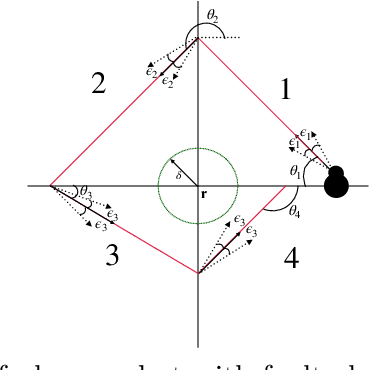
Abstract:In this paper, we study the probabilistic stability analysis of a subclass of stochastic hybrid systems, called the Planar Probabilistic Piecewise Constant Derivative Systems (Planar PPCD), where the continuous dynamics is deterministic, constant rate and planar, the discrete switching between the modes is probabilistic and happens at boundary of the invariant regions, and the continuous states are not reset during switching. These aptly model piecewise linear behaviors of planar robots. Our main result is an exact algorithm for deciding absolute and almost sure stability of Planar PPCD under some mild assumptions on mutual reachability between the states and the presence of non-zero probability self-loops. Our main idea is to reduce the stability problems on planar PPCD into corresponding problems on Discrete Time Markov Chains with edge weights. Our experimental results on planar robots with faulty angle actuator demonstrate the practical feasibility of this approach.
Bisimulations for Neural Network Reduction
Oct 07, 2021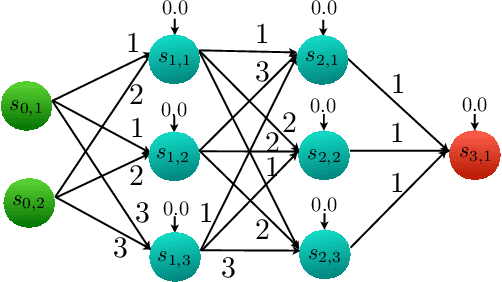
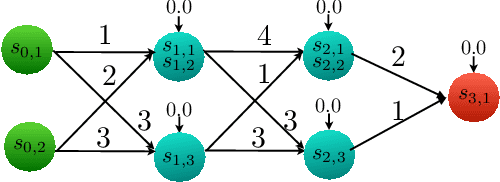
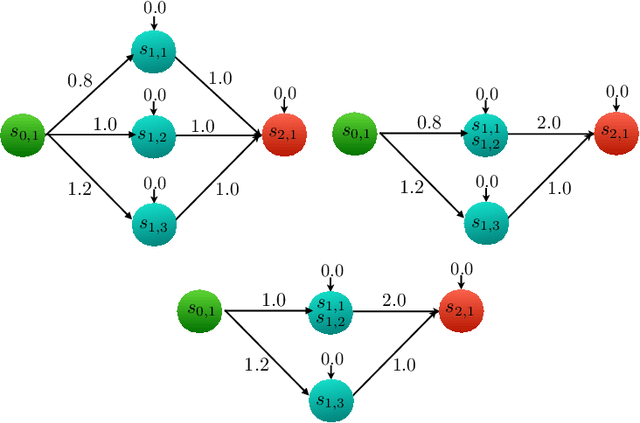
Abstract:We present a notion of bisimulation that induces a reduced network which is semantically equivalent to the given neural network. We provide a minimization algorithm to construct the smallest bisimulation equivalent network. Reductions that construct bisimulation equivalent neural networks are limited in the scale of reduction. We present an approximate notion of bisimulation that provides semantic closeness, rather than, semantic equivalence, and quantify semantic deviation between the neural networks that are approximately bisimilar. The latter provides a trade-off between the amount of reduction and deviations in the semantics.
Learning event-driven switched linear systems
Sep 27, 2020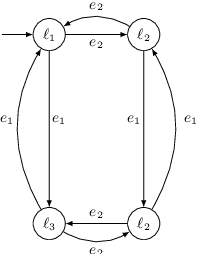

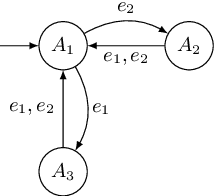
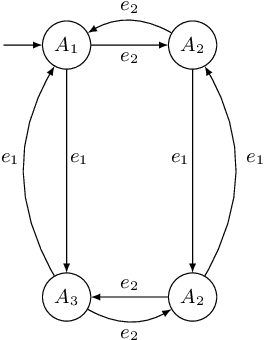
Abstract:We propose an automata theoretic learning algorithm for the identification of black-box switched linear systems whose switching logics are event-driven. A switched system is expressed by a deterministic finite automaton (FA) whose node labels are the subsystem matrices. With information about the dimensions of the matrices and the set of events, and with access to two oracles, that can simulate the system on a given input, and provide counter-examples when given an incorrect hypothesis automaton, we provide an algorithm that outputs the unknown FA. Our algorithm first uses the oracle to obtain the node labels of the system run on a given input sequence of events, and then extends Angluin's \(L^*\)-algorithm to determine the FA that accepts the language of the given FA. We demonstrate the performance of our learning algorithm on a set of benchmark examples.
Optimal tool path planning for 3D printing with spatio-temporal and thermal constraints
Jul 19, 2020
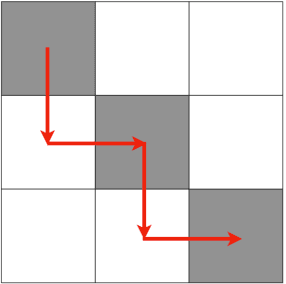
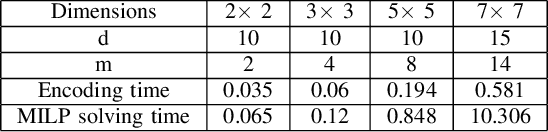
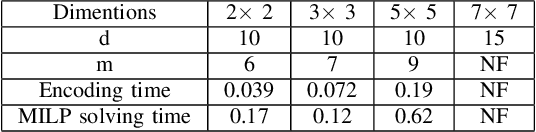
Abstract:In this paper, we address the problem of synthesizing optimal path plans in a 2D subject to spatio-temporal and thermal constraints. Our solution consists of reducing the path planning problem to a Mixed Integer Linear Programming (MILP) problem. The challenge is in encoding the implication constraints in the path planning problem using only conjunctions that are permitted by the MILP formulation. Our experimental analysis using an implementation of the encoding in a Python toolbox demonstrates the feasibility of our approach in generating the optimal plans.
Abstraction based Output Range Analysis for Neural Networks
Jul 18, 2020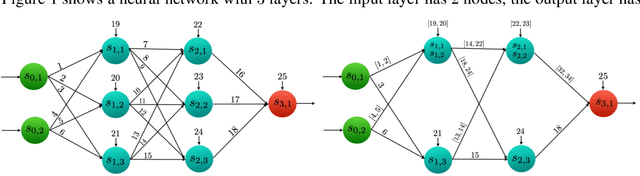
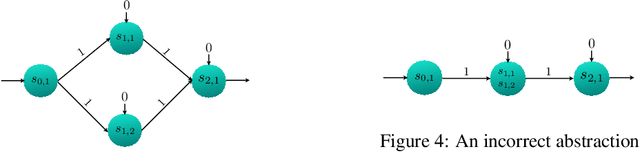

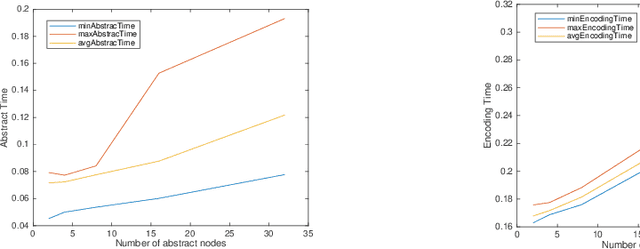
Abstract:In this paper, we consider the problem of output range analysis for feed-forward neural networks with ReLU activation functions. The existing approaches reduce the output range analysis problem to satisfiability and optimization solving, which are NP-hard problems, and whose computational complexity increases with the number of neurons in the network. To tackle the computational complexity, we present a novel abstraction technique that constructs a simpler neural network with fewer neurons, albeit with interval weights called interval neural network (INN), which over-approximates the output range of the given neural network. We reduce the output range analysis on the INNs to solving a mixed integer linear programming problem. Our experimental results highlight the trade-off between the computation time and the precision of the computed output range.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge