MATES: Model-Aware Data Selection for Efficient Pretraining with Data Influence Models

Pretraining data selection has the potential to improve language model pretraining efficiency by utilizing higher-quality data from massive web data corpora. Current data selection methods, which rely on either hand-crafted rules or larger reference models, are conducted statically and do not capture the evolving data preferences during pretraining. In this paper, we introduce model-aware data selection with data influence models (MATES), where a data influence model continuously adapts to the evolving data preferences of the pretraining model and then selects the data most effective for the current pretraining progress. Specifically, we fine-tune a small data influence model to approximate oracle data preference signals collected by locally probing the pretraining model and to select data accordingly for the next pretraining stage. Experiments on Pythia and the C4 dataset demonstrate that MATES significantly outperforms random data selection on extensive downstream tasks in both zero- and few-shot settings. It doubles the gains achieved by recent data selection approaches that leverage larger reference models and reduces the total FLOPs required to reach certain performances by half. Further analysis validates the ever-changing data preferences of pretraining models and the effectiveness of our data influence models to capture them. Our code is open-sourced at https://github.com/cxcscmu/MATES.

TLDR at SemEval-2024 Task 2: T5-generated clinical-Language summaries for DeBERTa Report Analysis

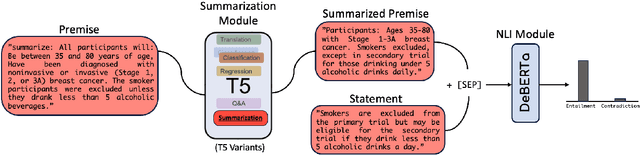
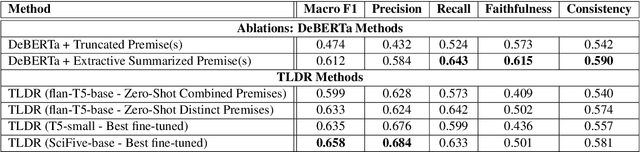
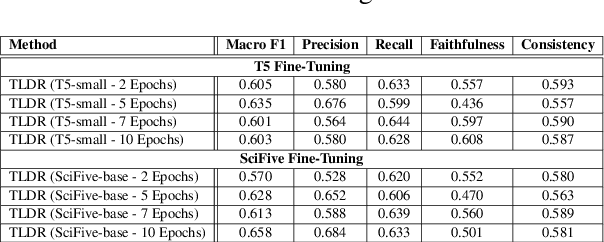
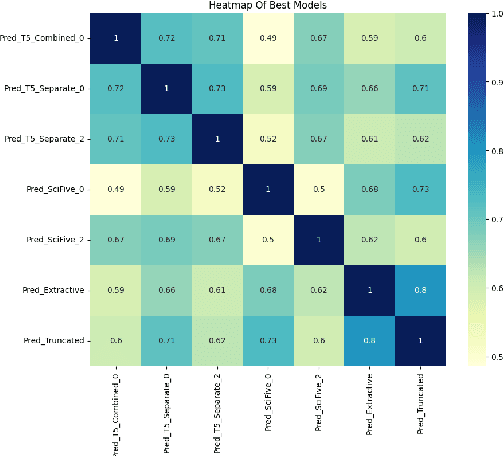
This paper introduces novel methodologies for the Natural Language Inference for Clinical Trials (NLI4CT) task. We present TLDR (T5-generated clinical-Language summaries for DeBERTa Report Analysis) which incorporates T5-model generated premise summaries for improved entailment and contradiction analysis in clinical NLI tasks. This approach overcomes the challenges posed by small context windows and lengthy premises, leading to a substantial improvement in Macro F1 scores: a 0.184 increase over truncated premises. Our comprehensive experimental evaluation, including detailed error analysis and ablations, confirms the superiority of TLDR in achieving consistency and faithfulness in predictions against semantically altered inputs.

Abstraction-based Probabilistic Stability Analysis of Polyhedral Probabilistic Hybrid Systems

In this paper, we consider the problem of probabilistic stability analysis of a subclass of Stochastic Hybrid Systems, namely, Polyhedral Probabilistic Hybrid Systems (PPHS), where the flow dynamics is given by a polyhedral inclusion, the discrete switching between modes happens probabilistically at the boundaries of their invariant regions and the continuous state is not reset during switching. We present an abstraction-based analysis framework that consists of constructing a finite Markov Decision Processes (MDP) such that verification of certain property on the finite MDP ensures the satisfaction of probabilistic stability on the PPHS. Further, we present a polynomial-time algorithm for verifying the corresponding property on the MDP. Our experimental analysis demonstrates the feasibility of the approach in successfully verifying probabilistic stability on PPHS of various dimensions and sizes.

Bayesian Statistical Model Checking for Multi-agent Systems using HyperPCTL*

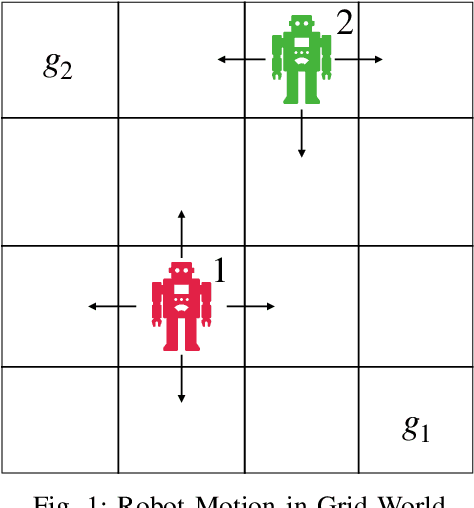
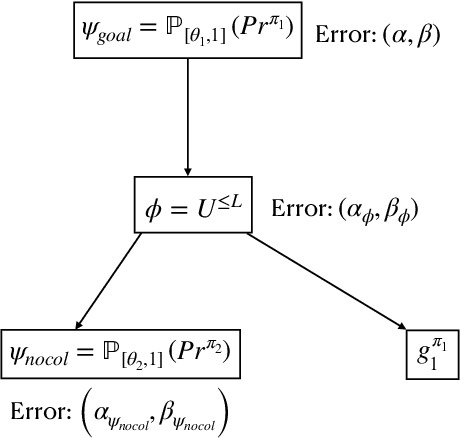
In this paper, we present a Bayesian method for statistical model checking (SMC) of probabilistic hyperproperties specified in the logic HyperPCTL* on discrete-time Markov chains (DTMCs). While SMC of HyperPCTL* using sequential probability ratio test (SPRT) has been explored before, we develop an alternative SMC algorithm based on Bayesian hypothesis testing. In comparison to PCTL*, verifying HyperPCTL* formulae is complex owing to their simultaneous interpretation on multiple paths of the DTMC. In addition, extending the bottom-up model-checking algorithm of the non-probabilistic setting is not straight forward due to the fact that SMC does not return exact answers to the satisfiability problems of subformulae, instead, it only returns correct answers with high-confidence. We propose a recursive algorithm for SMC of HyperPCTL* based on a modified Bayes' test that factors in the uncertainty in the recursive satisfiability results. We have implemented our algorithm in a Python toolbox, HyProVer, and compared our approach with the SPRT based SMC. Our experimental evaluation demonstrates that our Bayesian SMC algorithm performs better both in terms of the verification time and the number of samples required to deduce satisfiability of a given HyperPCTL* formula.

Probabilistic Stability Analysis of Planar Robots with Piecewise Constant Derivative Dynamics

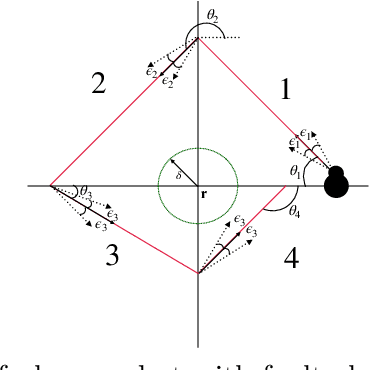
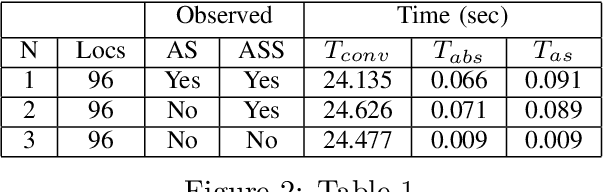
In this paper, we study the probabilistic stability analysis of a subclass of stochastic hybrid systems, called the Planar Probabilistic Piecewise Constant Derivative Systems (Planar PPCD), where the continuous dynamics is deterministic, constant rate and planar, the discrete switching between the modes is probabilistic and happens at boundary of the invariant regions, and the continuous states are not reset during switching. These aptly model piecewise linear behaviors of planar robots. Our main result is an exact algorithm for deciding absolute and almost sure stability of Planar PPCD under some mild assumptions on mutual reachability between the states and the presence of non-zero probability self-loops. Our main idea is to reduce the stability problems on planar PPCD into corresponding problems on Discrete Time Markov Chains with edge weights. Our experimental results on planar robots with faulty angle actuator demonstrate the practical feasibility of this approach.