Probabilistic Stability Analysis of Planar Robots with Piecewise Constant Derivative Dynamics
Paper and Code
Oct 08, 2021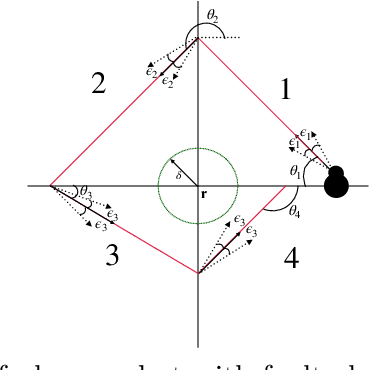
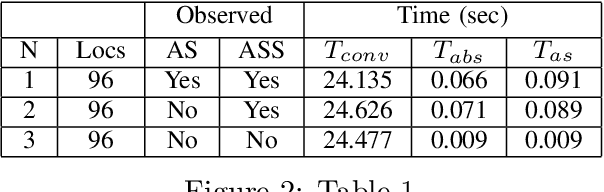
In this paper, we study the probabilistic stability analysis of a subclass of stochastic hybrid systems, called the Planar Probabilistic Piecewise Constant Derivative Systems (Planar PPCD), where the continuous dynamics is deterministic, constant rate and planar, the discrete switching between the modes is probabilistic and happens at boundary of the invariant regions, and the continuous states are not reset during switching. These aptly model piecewise linear behaviors of planar robots. Our main result is an exact algorithm for deciding absolute and almost sure stability of Planar PPCD under some mild assumptions on mutual reachability between the states and the presence of non-zero probability self-loops. Our main idea is to reduce the stability problems on planar PPCD into corresponding problems on Discrete Time Markov Chains with edge weights. Our experimental results on planar robots with faulty angle actuator demonstrate the practical feasibility of this approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge