Optimal tool path planning for 3D printing with spatio-temporal and thermal constraints

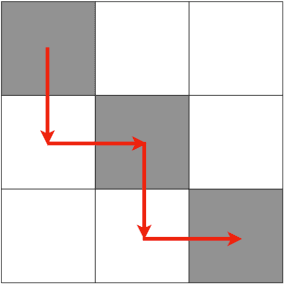
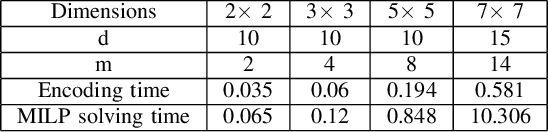
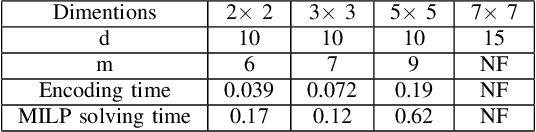
In this paper, we address the problem of synthesizing optimal path plans in a 2D subject to spatio-temporal and thermal constraints. Our solution consists of reducing the path planning problem to a Mixed Integer Linear Programming (MILP) problem. The challenge is in encoding the implication constraints in the path planning problem using only conjunctions that are permitted by the MILP formulation. Our experimental analysis using an implementation of the encoding in a Python toolbox demonstrates the feasibility of our approach in generating the optimal plans.

Abstraction based Output Range Analysis for Neural Networks

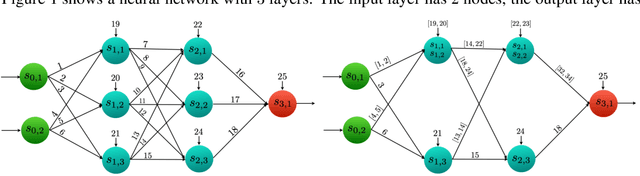
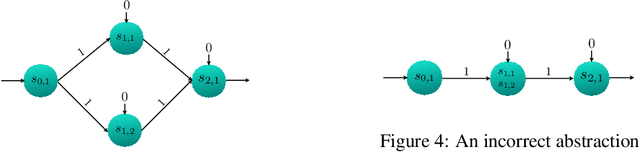
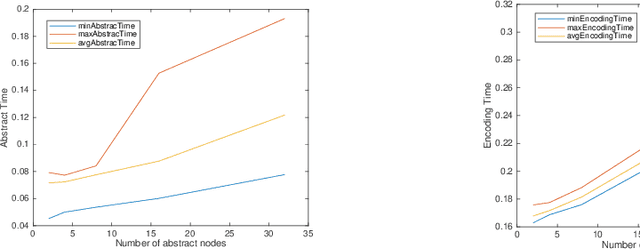
In this paper, we consider the problem of output range analysis for feed-forward neural networks with ReLU activation functions. The existing approaches reduce the output range analysis problem to satisfiability and optimization solving, which are NP-hard problems, and whose computational complexity increases with the number of neurons in the network. To tackle the computational complexity, we present a novel abstraction technique that constructs a simpler neural network with fewer neurons, albeit with interval weights called interval neural network (INN), which over-approximates the output range of the given neural network. We reduce the output range analysis on the INNs to solving a mixed integer linear programming problem. Our experimental results highlight the trade-off between the computation time and the precision of the computed output range.