Learning event-driven switched linear systems
Paper and Code
Sep 27, 2020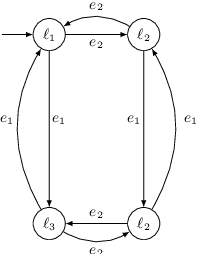

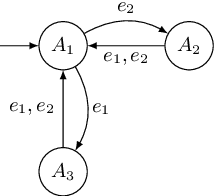
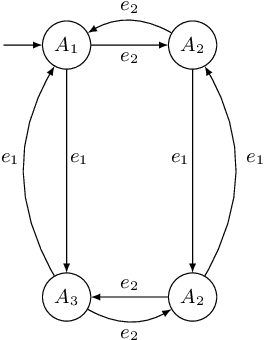
We propose an automata theoretic learning algorithm for the identification of black-box switched linear systems whose switching logics are event-driven. A switched system is expressed by a deterministic finite automaton (FA) whose node labels are the subsystem matrices. With information about the dimensions of the matrices and the set of events, and with access to two oracles, that can simulate the system on a given input, and provide counter-examples when given an incorrect hypothesis automaton, we provide an algorithm that outputs the unknown FA. Our algorithm first uses the oracle to obtain the node labels of the system run on a given input sequence of events, and then extends Angluin's \(L^*\)-algorithm to determine the FA that accepts the language of the given FA. We demonstrate the performance of our learning algorithm on a set of benchmark examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge