Learning event-driven switched linear systems

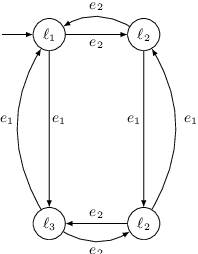
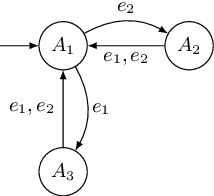
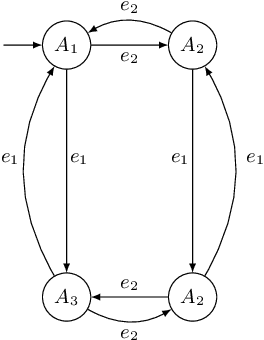
We propose an automata theoretic learning algorithm for the identification of black-box switched linear systems whose switching logics are event-driven. A switched system is expressed by a deterministic finite automaton (FA) whose node labels are the subsystem matrices. With information about the dimensions of the matrices and the set of events, and with access to two oracles, that can simulate the system on a given input, and provide counter-examples when given an incorrect hypothesis automaton, we provide an algorithm that outputs the unknown FA. Our algorithm first uses the oracle to obtain the node labels of the system run on a given input sequence of events, and then extends Angluin's \(L^*\)-algorithm to determine the FA that accepts the language of the given FA. We demonstrate the performance of our learning algorithm on a set of benchmark examples.

A reinforcement learning approach to hybrid control design

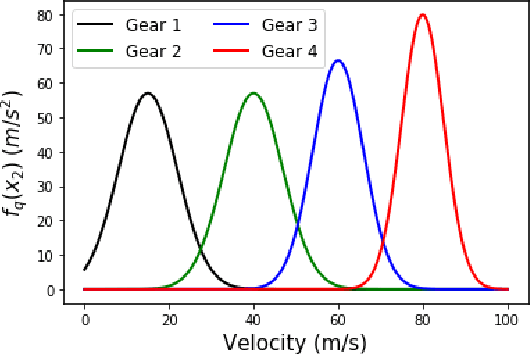
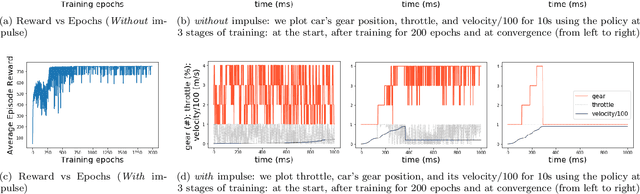
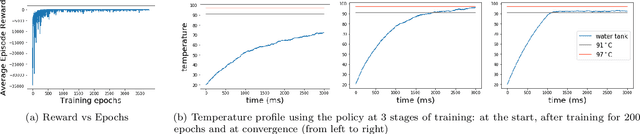
In this paper we design hybrid control policies for hybrid systems whose mathematical models are unknown. Our contributions are threefold. First, we propose a framework for modelling the hybrid control design problem as a single Markov Decision Process (MDP). This result facilitates the application of off-the-shelf algorithms from Reinforcement Learning (RL) literature towards designing optimal control policies. Second, we model a set of benchmark examples of hybrid control design problem in the proposed MDP framework. Third, we adapt the recently proposed Proximal Policy Optimisation (PPO) algorithm for the hybrid action space and apply it to the above set of problems. It is observed that in each case the algorithm converges and finds the optimal policy.

Data-based design of stabilizing switching signals for discrete-time switched linear systems

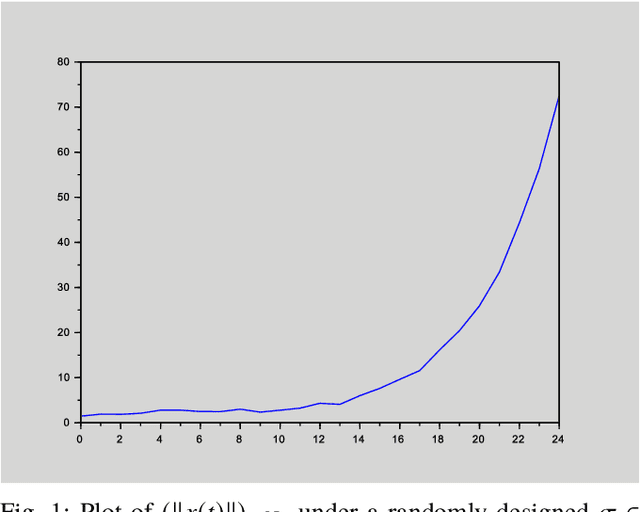
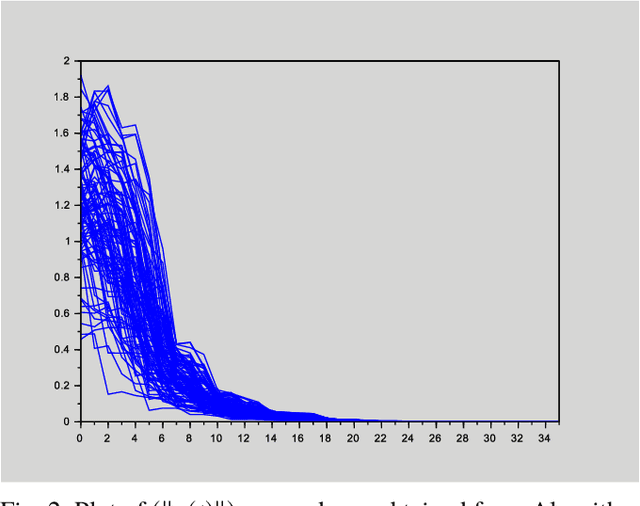
This paper deals with stabilization of discrete-time switched linear systems when explicit knowledge of the state-space models of their subsystems are not available. Given the sets of indices of the stable and unstable subsystems, the set of admissible switches between the subsystems, the admissible dwell times on the subsystems and a simulation model from which finite traces of state trajectories of the switched system can be collected, we devise an algorithm that designs periodic switching signals which preserve stability of the resulting switched system. We combine two ingredients: (a) data-based stability analysis of discrete-time linear systems and (b) multiple Lyapunov-like functions and graph walks based design of stabilizing switching signals, for this purpose. A numerical example is presented to demonstrate the proposed algorithm.

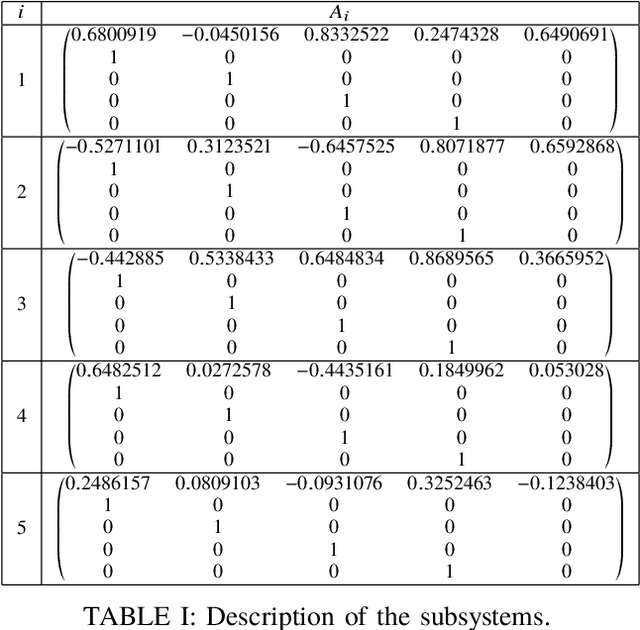
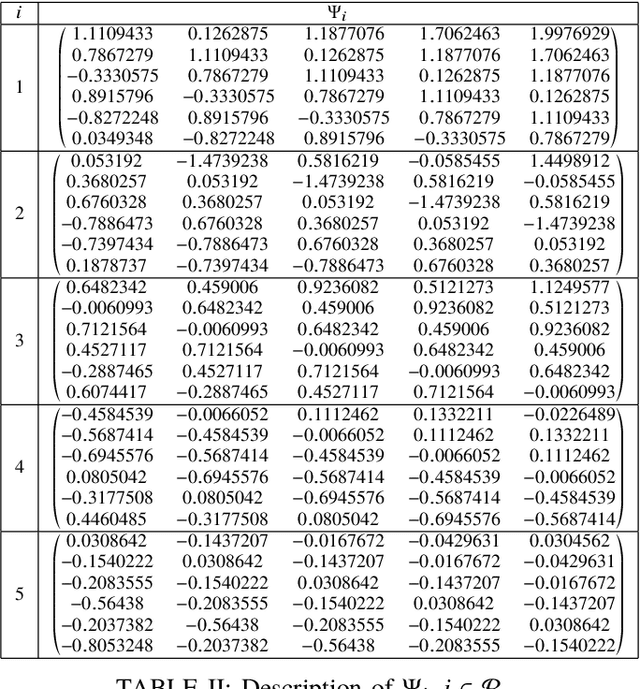
Data-based computation of stabilizing minimum dwell times for discrete-time switched linear systems

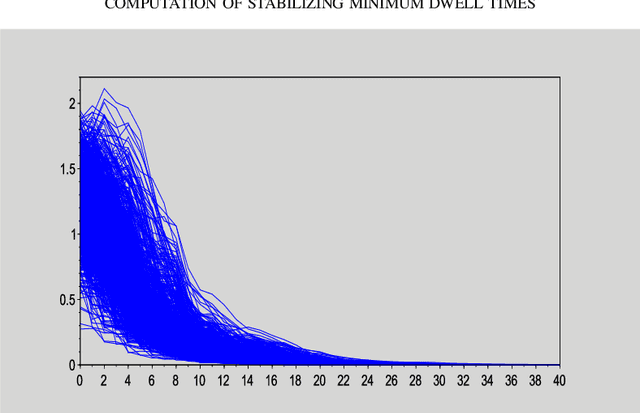
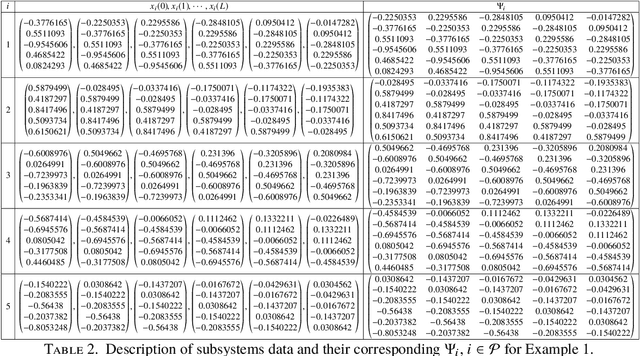
We present an algorithm to compute stabilizing minimum dwell times for discrete-time switched linear systems without the explicit knowledge of state-space models of their subsystems. Given a set of finite traces of state trajectories of the subsystems that satisfies certain properties, our algorithm involves the following tasks: first, multiple Lyapunov functions are designed from the given data; second, a set of relevant scalars is computed from these functions; and third, a stabilizing minimum dwell time is determined as a function of these scalars. A numerical example is presented to demonstrate the proposed algorithm.