Data-based computation of stabilizing minimum dwell times for discrete-time switched linear systems

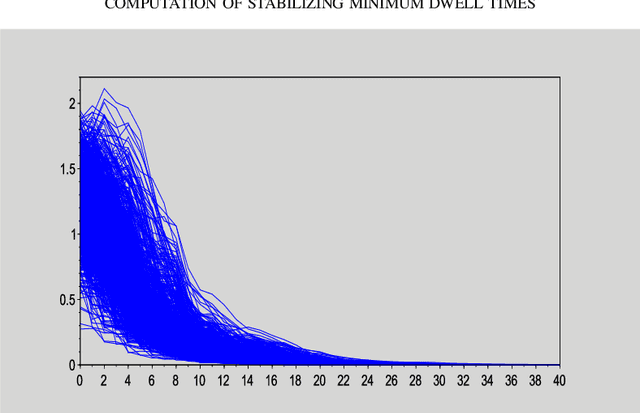
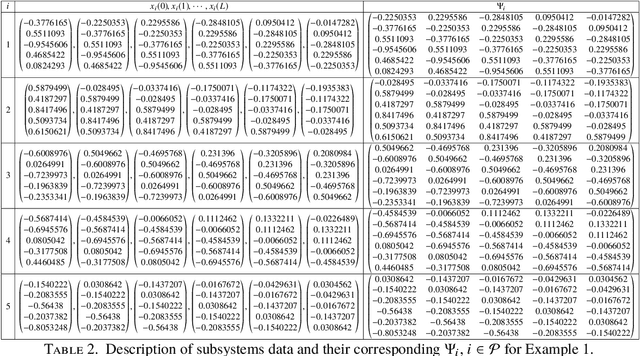
We present an algorithm to compute stabilizing minimum dwell times for discrete-time switched linear systems without the explicit knowledge of state-space models of their subsystems. Given a set of finite traces of state trajectories of the subsystems that satisfies certain properties, our algorithm involves the following tasks: first, multiple Lyapunov functions are designed from the given data; second, a set of relevant scalars is computed from these functions; and third, a stabilizing minimum dwell time is determined as a function of these scalars. A numerical example is presented to demonstrate the proposed algorithm.