Data-based design of stabilizing switching signals for discrete-time switched linear systems

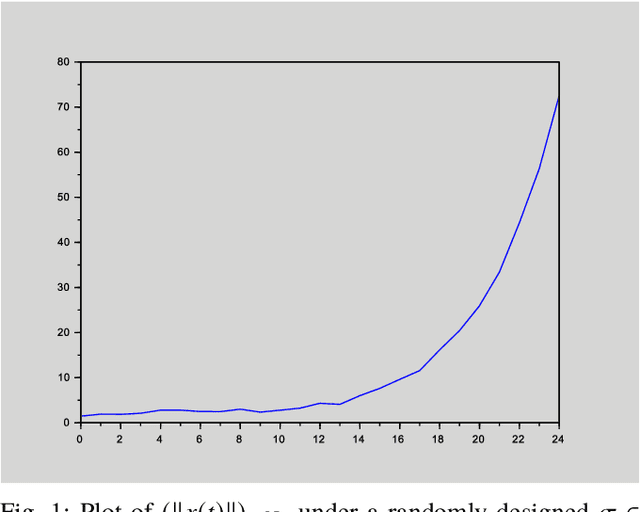
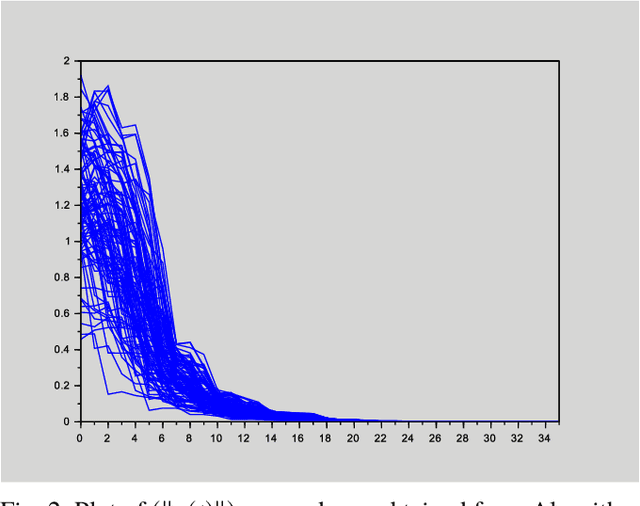
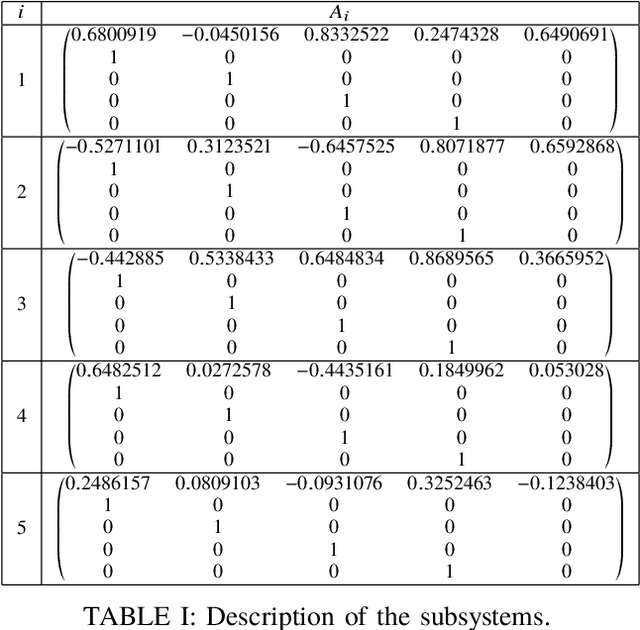
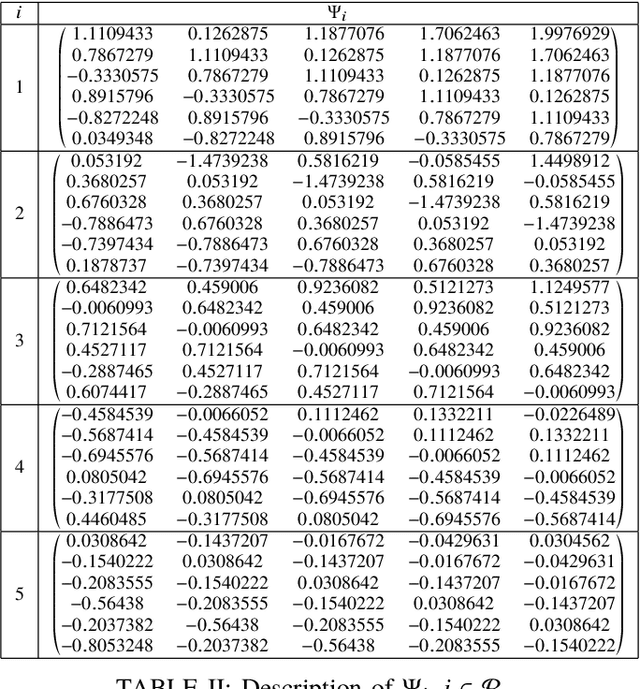
This paper deals with stabilization of discrete-time switched linear systems when explicit knowledge of the state-space models of their subsystems are not available. Given the sets of indices of the stable and unstable subsystems, the set of admissible switches between the subsystems, the admissible dwell times on the subsystems and a simulation model from which finite traces of state trajectories of the switched system can be collected, we devise an algorithm that designs periodic switching signals which preserve stability of the resulting switched system. We combine two ingredients: (a) data-based stability analysis of discrete-time linear systems and (b) multiple Lyapunov-like functions and graph walks based design of stabilizing switching signals, for this purpose. A numerical example is presented to demonstrate the proposed algorithm.