k*-Nearest Neighbors: From Global to Local

The weighted k-nearest neighbors algorithm is one of the most fundamental non-parametric methods in pattern recognition and machine learning. The question of setting the optimal number of neighbors as well as the optimal weights has received much attention throughout the years, nevertheless this problem seems to have remained unsettled. In this paper we offer a simple approach to locally weighted regression/classification, where we make the bias-variance tradeoff explicit. Our formulation enables us to phrase a notion of optimal weights, and to efficiently find these weights as well as the optimal number of neighbors efficiently and adaptively, for each data point whose value we wish to estimate. The applicability of our approach is demonstrated on several datasets, showing superior performance over standard locally weighted methods.

Budget-Constrained Item Cold-Start Handling in Collaborative Filtering Recommenders via Optimal Design

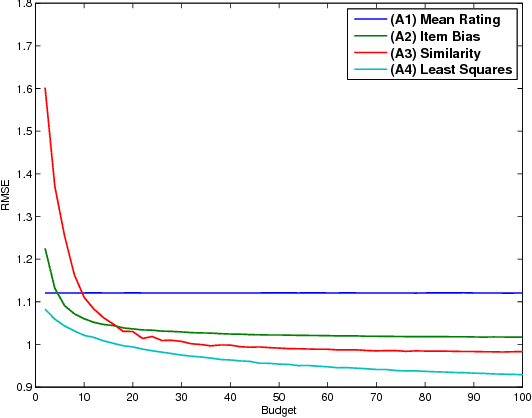
It is well known that collaborative filtering (CF) based recommender systems provide better modeling of users and items associated with considerable rating history. The lack of historical ratings results in the user and the item cold-start problems. The latter is the main focus of this work. Most of the current literature addresses this problem by integrating content-based recommendation techniques to model the new item. However, in many cases such content is not available, and the question arises is whether this problem can be mitigated using CF techniques only. We formalize this problem as an optimization problem: given a new item, a pool of available users, and a budget constraint, select which users to assign with the task of rating the new item in order to minimize the prediction error of our model. We show that the objective function is monotone-supermodular, and propose efficient optimal design based algorithms that attain an approximation to its optimum. Our findings are verified by an empirical study using the Netflix dataset, where the proposed algorithms outperform several baselines for the problem at hand.

Online Convex Optimization Against Adversaries with Memory and Application to Statistical Arbitrage

The framework of online learning with memory naturally captures learning problems with temporal constraints, and was previously studied for the experts setting. In this work we extend the notion of learning with memory to the general Online Convex Optimization (OCO) framework, and present two algorithms that attain low regret. The first algorithm applies to Lipschitz continuous loss functions, obtaining optimal regret bounds for both convex and strongly convex losses. The second algorithm attains the optimal regret bounds and applies more broadly to convex losses without requiring Lipschitz continuity, yet is more complicated to implement. We complement our theoretic results with an application to statistical arbitrage in finance: we devise algorithms for constructing mean-reverting portfolios.

Online Learning for Time Series Prediction

In this paper we address the problem of predicting a time series using the ARMA (autoregressive moving average) model, under minimal assumptions on the noise terms. Using regret minimization techniques, we develop effective online learning algorithms for the prediction problem, without assuming that the noise terms are Gaussian, identically distributed or even independent. Furthermore, we show that our algorithm's performances asymptotically approaches the performance of the best ARMA model in hindsight.