Omar Costilla-Reyes
Predicting Treatment Response in Body Dysmorphic Disorder with Interpretable Machine Learning
Mar 13, 2025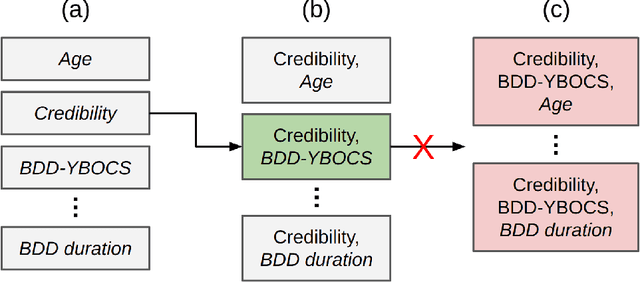



Abstract:Body Dysmorphic Disorder (BDD) is a highly prevalent and frequently underdiagnosed condition characterized by persistent, intrusive preoccupations with perceived defects in physical appearance. In this extended analysis, we employ multiple machine learning approaches to predict treatment outcomes -- specifically treatment response and remission -- with an emphasis on interpretability to ensure clinical relevance and utility. Across the various models investigated, treatment credibility emerged as the most potent predictor, surpassing traditional markers such as baseline symptom severity or comorbid conditions. Notably, while simpler models (e.g., logistic regression and support vector machines) achieved competitive predictive performance, decision tree analyses provided unique insights by revealing clinically interpretable threshold values in credibility scores. These thresholds can serve as practical guideposts for clinicians when tailoring interventions or allocating treatment resources. We further contextualize our findings within the broader literature on BDD, addressing technology-based therapeutics, digital interventions, and the psychosocial determinants of treatment engagement. An extensive array of references situates our results within current research on BDD prevalence, suicidality risks, and digital innovation. Our work underscores the potential of integrating rigorous statistical methodologies with transparent machine learning models. By systematically identifying modifiable predictors -- such as treatment credibility -- we propose a pathway toward more targeted, personalized, and ultimately efficacious interventions for individuals with BDD.
MathDSL: A Domain-Specific Language for Concise Mathematical Solutions Via Program Synthesis
Sep 26, 2024Abstract:We present MathDSL, a Domain-Specific Language (DSL) for mathematical equation solving, which, when deployed in program synthesis models, outperforms state-of-the-art reinforcement-learning-based methods. We also introduce a quantitative metric for measuring the conciseness of a mathematical solution and demonstrate the improvement in the quality of generated solutions compared to other methods. Our system demonstrates that a program synthesis system (DreamCoder) using MathDSL can generate programs that solve linear equations with greater accuracy and conciseness than using reinforcement learning systems. Additionally, we demonstrate that if we use the action spaces of previous reinforcement learning systems as DSLs, MathDSL outperforms the action-space-DSLs. We use DreamCoder to store equation-solving strategies as learned abstractions in its program library and demonstrate that by using MathDSL, these can be converted into human-interpretable solution strategies that could have applications in mathematical education.
Symbolic Regression with a Learned Concept Library
Sep 14, 2024


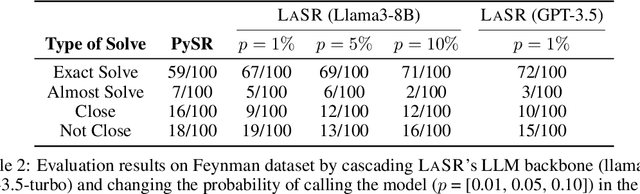
Abstract:We present a novel method for symbolic regression (SR), the task of searching for compact programmatic hypotheses that best explain a dataset. The problem is commonly solved using genetic algorithms; we show that we can enhance such methods by inducing a library of abstract textual concepts. Our algorithm, called LaSR, uses zero-shot queries to a large language model (LLM) to discover and evolve concepts occurring in known high-performing hypotheses. We discover new hypotheses using a mix of standard evolutionary steps and LLM-guided steps (obtained through zero-shot LLM queries) conditioned on discovered concepts. Once discovered, hypotheses are used in a new round of concept abstraction and evolution. We validate LaSR on the Feynman equations, a popular SR benchmark, as well as a set of synthetic tasks. On these benchmarks, LaSR substantially outperforms a variety of state-of-the-art SR approaches based on deep learning and evolutionary algorithms. Moreover, we show that LaSR can be used to discover a novel and powerful scaling law for LLMs.
Counterfactual Explanations and Predictive Models to Enhance Clinical Decision-Making in Schizophrenia using Digital Phenotyping
Jun 06, 2023



Abstract:Clinical practice in psychiatry is burdened with the increased demand for healthcare services and the scarce resources available. New paradigms of health data powered with machine learning techniques could open the possibility to improve clinical workflow in critical stages of clinical assessment and treatment in psychiatry. In this work, we propose a machine learning system capable of predicting, detecting, and explaining individual changes in symptoms of patients with Schizophrenia by using behavioral digital phenotyping data. We forecast symptoms of patients with an error rate below 10%. The system detects decreases in symptoms using changepoint algorithms and uses counterfactual explanations as a recourse in a simulated continuous monitoring scenario in healthcare. Overall, this study offers valuable insights into the performance and potential of counterfactual explanations, predictive models, and change-point detection within a simulated clinical workflow. These findings lay the foundation for further research to explore additional facets of the workflow, aiming to enhance its effectiveness and applicability in real-world healthcare settings. By leveraging these components, the goal is to develop an actionable, interpretable, and trustworthy integrative decision support system that combines real-time clinical assessments with sensor-based inputs.
LEMMA: Bootstrapping High-Level Mathematical Reasoning with Learned Symbolic Abstractions
Nov 16, 2022Abstract:Humans tame the complexity of mathematical reasoning by developing hierarchies of abstractions. With proper abstractions, solutions to hard problems can be expressed concisely, thus making them more likely to be found. In this paper, we propose Learning Mathematical Abstractions (LEMMA): an algorithm that implements this idea for reinforcement learning agents in mathematical domains. LEMMA augments Expert Iteration with an abstraction step, where solutions found so far are revisited and rewritten in terms of new higher-level actions, which then become available to solve new problems. We evaluate LEMMA on two mathematical reasoning tasks--equation solving and fraction simplification--in a step-by-step fashion. In these two domains, LEMMA improves the ability of an existing agent, both solving more problems and generalizing more effectively to harder problems than those seen during training.
Neurosymbolic Programming for Science
Oct 10, 2022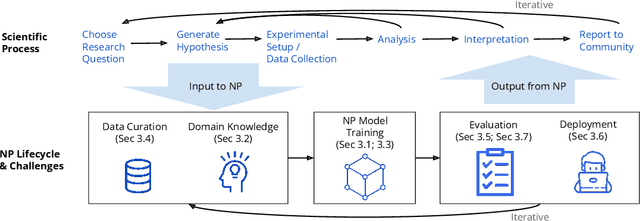
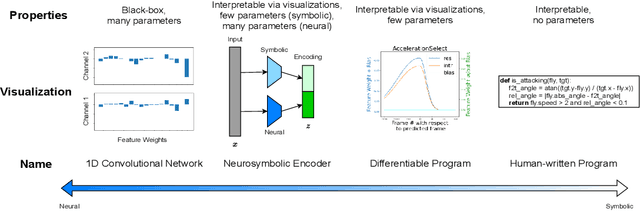
Abstract:Neurosymbolic Programming (NP) techniques have the potential to accelerate scientific discovery across fields. These models combine neural and symbolic components to learn complex patterns and representations from data, using high-level concepts or known constraints. As a result, NP techniques can interface with symbolic domain knowledge from scientists, such as prior knowledge and experimental context, to produce interpretable outputs. Here, we identify opportunities and challenges between current NP models and scientific workflows, with real-world examples from behavior analysis in science. We define concrete next steps to move the NP for science field forward, to enable its use broadly for workflows across the natural and social sciences.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge