Olivier Goudet
Black-Box Combinatorial Optimization with Order-Invariant Reinforcement Learning
Oct 02, 2025Abstract:We introduce an order-invariant reinforcement learning framework for black-box combinatorial optimization. Classical estimation-of-distribution algorithms (EDAs) often rely on learning explicit variable dependency graphs, which can be costly and fail to capture complex interactions efficiently. In contrast, we parameterize a multivariate autoregressive generative model trained without a fixed variable ordering. By sampling random generation orders during training - a form of information-preserving dropout - the model is encouraged to be invariant to variable order, promoting search-space diversity and shaping the model to focus on the most relevant variable dependencies, improving sample efficiency. We adapt Generalized Reinforcement Policy Optimization (GRPO) to this setting, providing stable policy-gradient updates from scale-invariant advantages. Across a wide range of benchmark algorithms and problem instances of varying sizes, our method frequently achieves the best performance and consistently avoids catastrophic failures.
Discovering new robust local search algorithms with neuro-evolution
Jan 08, 2025



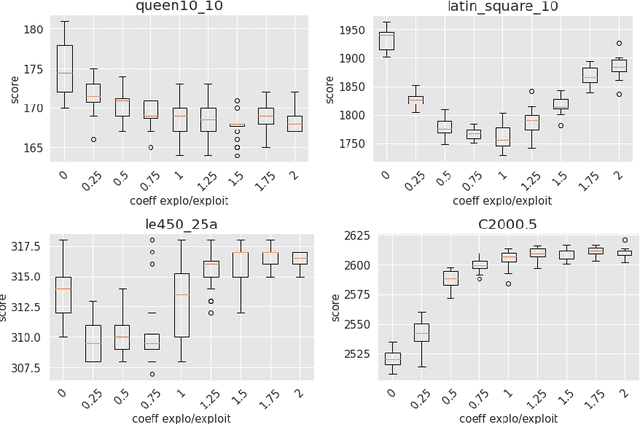
Abstract:This paper explores a novel approach aimed at overcoming existing challenges in the realm of local search algorithms. Our aim is to improve the decision process that takes place within a local search algorithm so as to make the best possible transitions in the neighborhood at each iteration. To improve this process, we propose to use a neural network that has the same input information as conventional local search algorithms. In this paper, which is an extension of the work [Goudet et al. 2024] presented at EvoCOP2024, we investigate different ways of representing this information so as to make the algorithm as efficient as possible but also robust to monotonic transformations of the problem objective function. To assess the efficiency of this approach, we develop an experimental setup centered around NK landscape problems, offering the flexibility to adjust problem size and ruggedness. This approach offers a promising avenue for the emergence of new local search algorithms and the improvement of their problem-solving capabilities for black-box problems.
Deinterleaving of Discrete Renewal Process Mixtures with Application to Electronic Support Measures
Feb 14, 2024Abstract:In this paper, we propose a new deinterleaving method for mixtures of discrete renewal Markov chains. This method relies on the maximization of a penalized likelihood score. It exploits all available information about both the sequence of the different symbols and their arrival times. A theoretical analysis is carried out to prove that minimizing this score allows to recover the true partition of symbols in the large sample limit, under mild conditions on the component processes. This theoretical analysis is then validated by experiments on synthetic data. Finally, the method is applied to deinterleave pulse trains received from different emitters in a RESM (Radar Electronic Support Measurements) context and we show that the proposed method competes favorably with state-of-the-art methods on simulated warfare datasets.
Combining Monte Carlo Tree Search and Heuristic Search for Weighted Vertex Coloring
Apr 24, 2023Abstract:This work investigates the Monte Carlo Tree Search (MCTS) method combined with dedicated heuristics for solving the Weighted Vertex Coloring Problem. In addition to the basic MCTS algorithm, we study several MCTS variants where the conventional random simulation is replaced by other simulation strategies including greedy and local search heuristics. We conduct experiments on well-known benchmark instances to assess these combined MCTS variants. We provide empirical evidence to shed light on the advantages and limits of each simulation strategy. This is an extension of the work of Grelier and al. presented at EvoCOP2022.
On Monte Carlo Tree Search for Weighted Vertex Coloring
Feb 03, 2022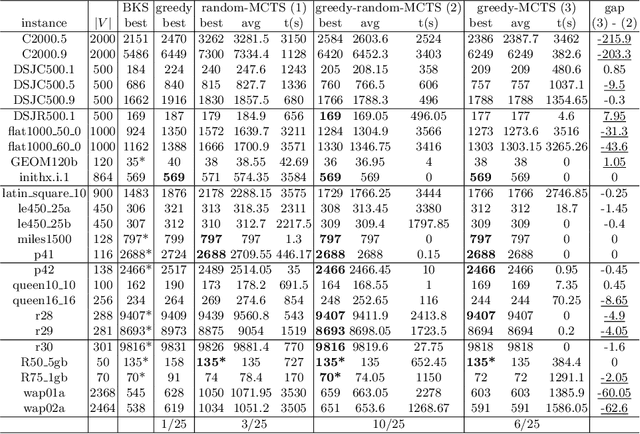
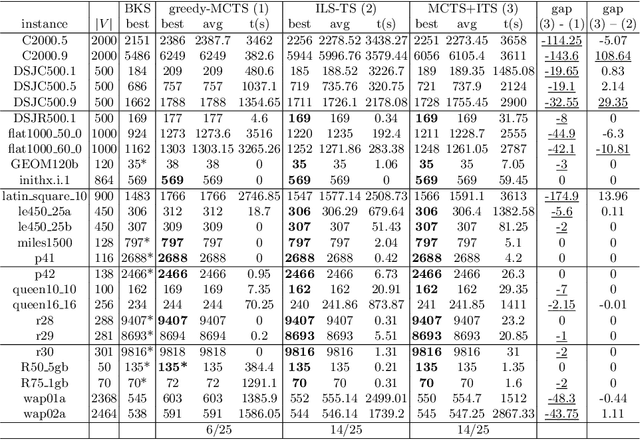
Abstract:This work presents the first study of using the popular Monte Carlo Tree Search (MCTS) method combined with dedicated heuristics for solving the Weighted Vertex Coloring Problem. Starting with the basic MCTS algorithm, we gradually introduce a number of algorithmic variants where MCTS is extended by various simulation strategies including greedy and local search heuristics. We conduct experiments on well-known benchmark instances to assess the value of each studied combination. We also provide empirical evidence to shed light on the advantages and limits of each strategy.
A deep learning guided memetic framework for graph coloring problems
Sep 13, 2021
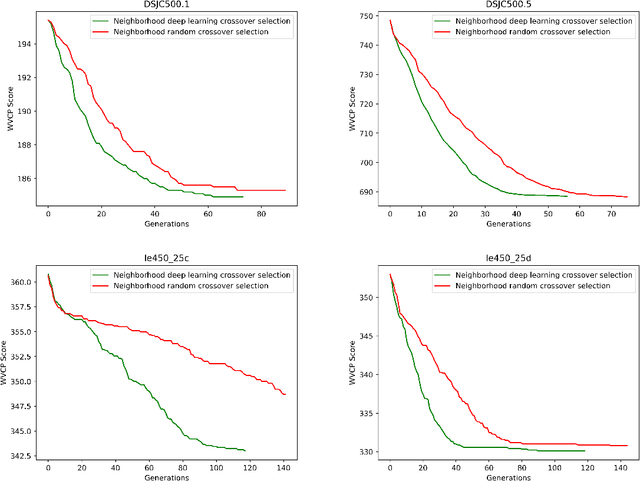
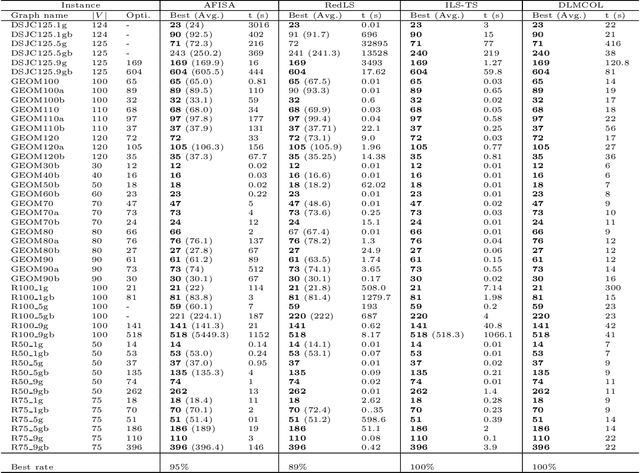
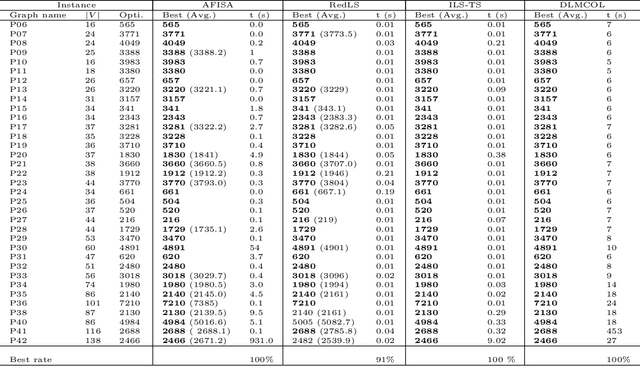
Abstract:Given an undirected graph $G=(V,E)$ with a set of vertices $V$ and a set of edges $E$, a graph coloring problem involves finding a partition of the vertices into different independent sets. In this paper we present a new framework which combines a deep neural network with the best tools of "classical" metaheuristics for graph coloring. The proposed algorithm is evaluated on the weighted graph coloring problem and computational results show that the proposed approach allows to obtain new upper bounds for medium and large graphs. A study of the contribution of deep learning in the algorithm highlights that it is possible to learn relevant patterns useful to obtain better solutions to this problem.
Massively parallel hybrid search for the partial Latin square extension problem
Mar 18, 2021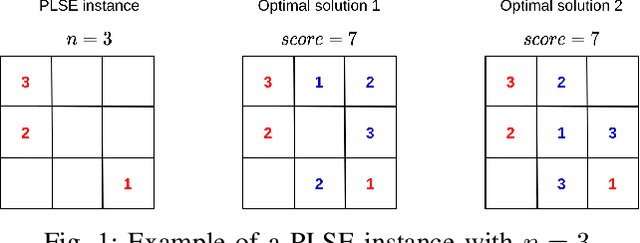
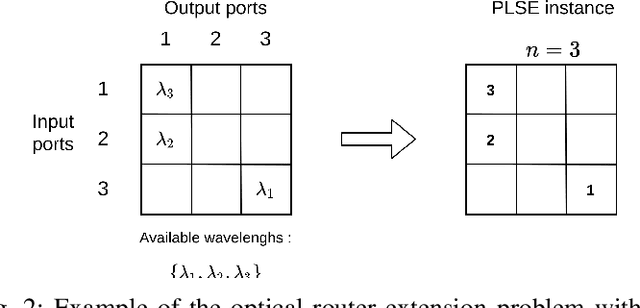
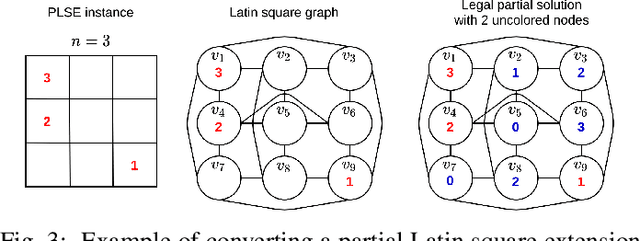
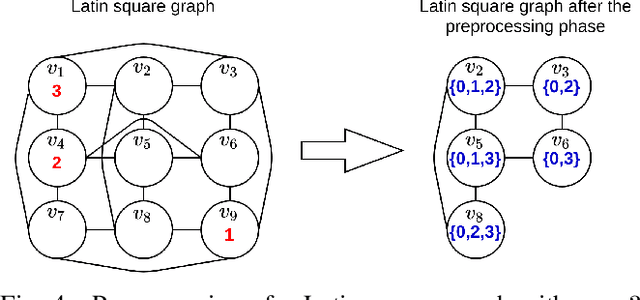
Abstract:The partial Latin square extension problem is to fill as many as possible empty cells of a partially filled Latin square. This problem is a useful model for a wide range of relevant applications in diverse domains. This paper presents the first massively parallel hybrid search algorithm for this computationally challenging problem based on a transformation of the problem to partial graph coloring. The algorithm features the following original elements. Based on a very large population (with more than $10^4$ individuals) and modern graphical processing units, the algorithm performs many local searches in parallel to ensure an intensified exploitation of the search space. It employs a dedicated crossover with a specific parent matching strategy to create a large number of diversified and information-preserving offspring at each generation. Extensive experiments on 1800 benchmark instances show a high competitiveness of the algorithm compared with the current best performing methods. Competitive results are also reported on the related Latin square completion problem. Analyses are performed to shed lights on the understanding of the main algorithmic components. The code of the algorithm will be made publicly available.
On the study of the Beran estimator for generalized censoring indicators
Sep 03, 2020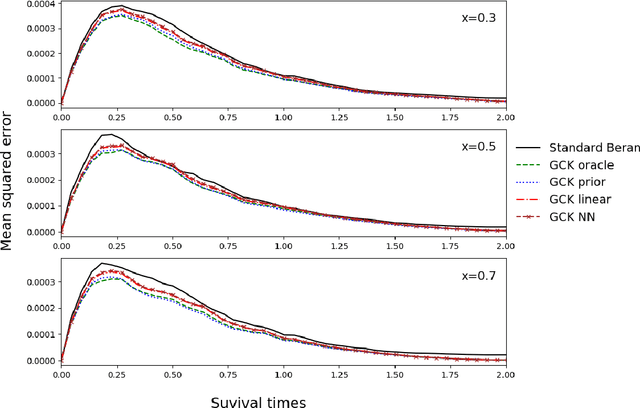

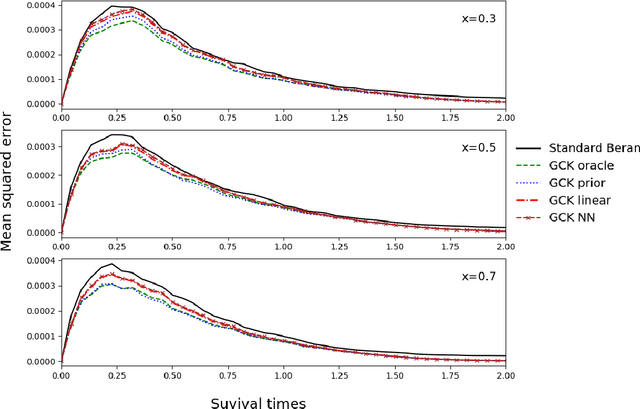

Abstract:Along with the analysis of time-to-event data, it is common to assume that only partial information is given at hand. In the presence of right-censored data with covariates, the conditional Kaplan-Meier estimator (also referred as the Beran estimator) is known to propose a consistent estimate for the lifetimes conditional survival function. However, a necessary condition is the clear knowledge of whether each individual is censored or not, although, this information might be incomplete or even totally absent in practice. We thus propose a study on the Beran estimator when the censoring indicator is not clearly specified. From this, we provide a new estimator for the conditional survival function and establish its asymptotic normality under mild conditions. We further study the supervised learning problem where the conditional survival function is to be predicted with no censorship indicators. To this aim, we investigate various approaches estimating the conditional expectation for the censoring indicator. Along with the theoretical results, we illustrate how the estimators work for small samples by means of a simulation study and show their practical applicability with the analysis of synthetic data and the study of real data for the prognosis of monoclonal gammopathy.
Gradient Descent based Weight Learning for Grouping Problems: Application on Graph Coloring and Equitable Graph Coloring
Sep 05, 2019


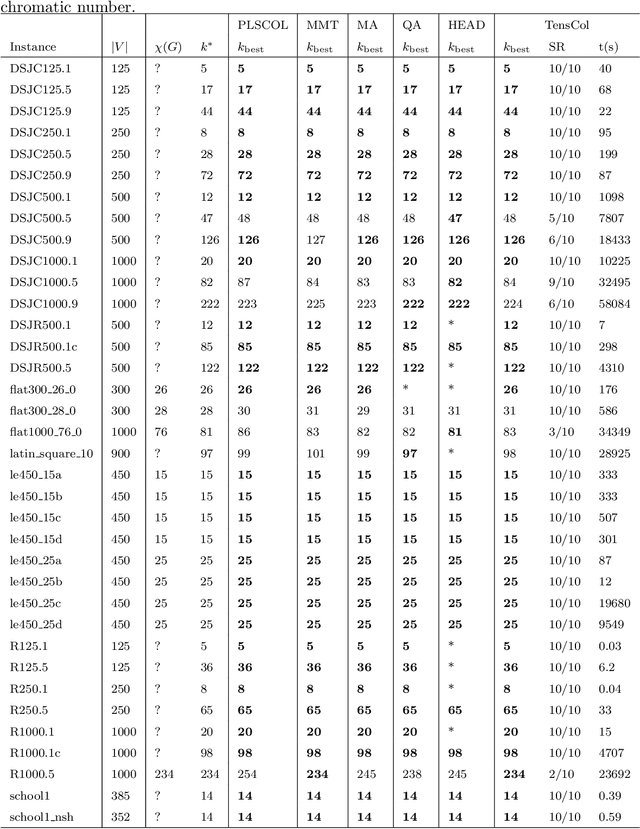
Abstract:A grouping problem involves partitioning a set of items into mutually disjoint groups or clusters according to some guiding decision criteria and imperative constraints. Grouping problems have many relevant applications and are computationally difficult. In this work, we present a general weight learning based optimization framework for solving grouping problems. The central idea of our approach is to formulate the task of seeking a solution as a real-valued weight matrix learning problem that is solved by first order gradient descent. A practical implementation of this framework is proposed with tensor calculus in order to benefit from parallel computing on GPU devices. To show its potential for tackling difficult problems, we apply the approach to two typical and well-known grouping problems (graph coloring and equitable graph coloring). We present large computational experiments and comparisons on popular benchmarks and report improved best-known results (new upper bounds) for several large graphs.
Causal Discovery Toolbox: Uncover causal relationships in Python
Mar 06, 2019
Abstract:This paper presents a new open source Python framework for causal discovery from observational data and domain background knowledge, aimed at causal graph and causal mechanism modeling. The 'cdt' package implements the end-to-end approach, recovering the direct dependencies (the skeleton of the causal graph) and the causal relationships between variables. It includes algorithms from the 'Bnlearn' and 'Pcalg' packages, together with algorithms for pairwise causal discovery such as ANM. 'cdt' is available under the MIT License at https://github.com/Diviyan-Kalainathan/CausalDiscoveryToolbox.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge